Matrix
행렬의 기본
Linear Algebra를 통해 해를 구할때 관점
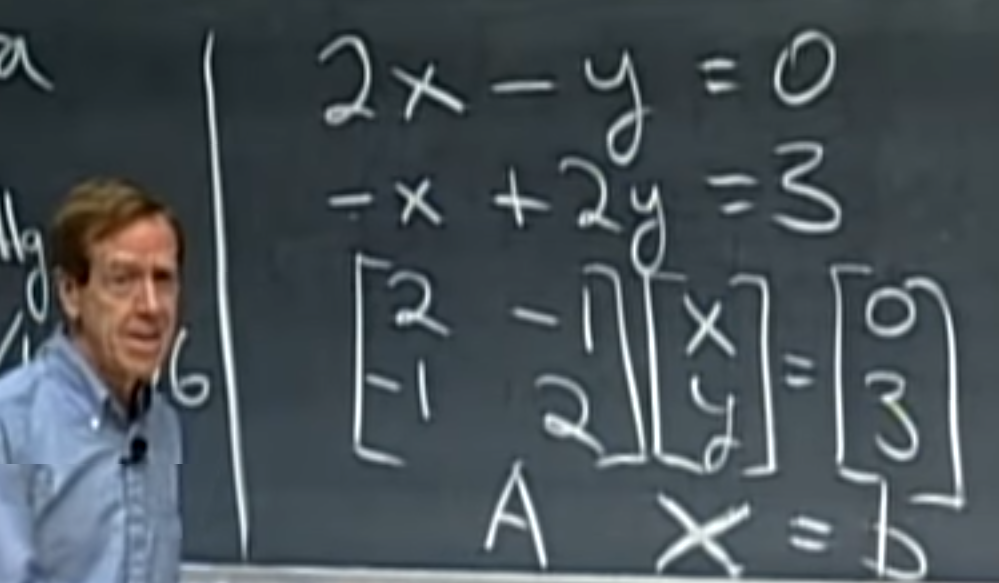
문제를 보는 관점
- Row 방향:
직선/평면..의 방정식으로 (dot product, 내적)
- Column방향:
벡터들의 선형결합으로 (Linear combination)
Transpose M(전치행렬) : t(A)
: 행과 열을 교환하여 얻는 행렬, diagonal 을 축으로 off-diagonal 을 반사대칭한 행렬
-
임의의 행렬A 에 대해, A의 transpose M을 곱하면 항상 Symmetric M이 나온다.
Inverse M(역행렬) : solve(A)
: 곱해서 단위행렬이 나오게 하는 행렬
크기가 같고 역행렬이 존재하는 두 행렬 A와 B에 대해 다음이 성립
Determinent (행렬식) : det(A)
에서 A의 역원이 존재해야, 해를 구할수 있기 때문에, A의 역원의 존재하는지 확인하는 방법으로 행렬식을 사용한다.
즉, det(A)는 0이 아니어야 해가 있다.
det(A)는 0이 아니다 = 역원이 존재한다 = Invertiblility (가역성) = Non-singularity = column이 선형독립이다 = Rank가 column수와 같다
det(A)는 기하학적으로 의 두벡터 r1=(a,b) , r2=(c,d) 가 만드는 평행사변형의 넓이
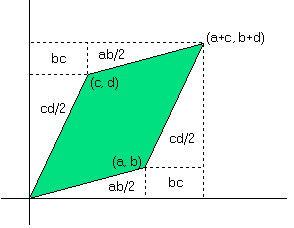
즉, A가 한변의 길이가 1이고, 넓이 1인 정사각형을, 넓이 ad-bc인 평행사변형으로 선형변환한 것이라면,
역행렬 은 다시 역변환을 통해 정사각형 I 로 되돌려주는 선행변환이다.
Rank (계수) : qr(A)$rank
선형독립인 열 또는 행의 갯수
Decomposition (=Factorization, 인수분해) : svd(A), qr(A), chol(A)
임의한 한 M을 여러 M의 곱으로 표현하는 것 => 편한 계산, 단순화
Matrix 종류
Square M(정사각행렬)
: row와 column이 같은 수의 행렬
Symmetric M(대칭행렬)
: 즉
ex) Covariance M
Orthogonal M(직교행렬)
: 즉,
(
)
:임의의 행렬A 에 대해, A의 transpose M을 곱하면 항상 Symmetric M이 나오는데, 그 대칭행렬이 Identity M이면 직교한다고 한다.
Diagonal M(대각행렬)
: Main diagonal이 상관없이 , off diagonal 는 0을 값을 갖는 정사각행렬
계산을 간단하게 만드는 좋은 성질을 가지고 있기 때문에, EVD(Eigenvalue Decomposition)과 같은 방법으로 행렬을 대각행렬로 만드는 방법이 많이 사용되었다.
Ar = Lr
r 는 eigen-vector, L는 eigen-value의 대각행렬일때, r는 Av 와 평행하다.
즉, 선형변환해 주는 A행렬을 어떤 r 에 곱했을때 v와 평행한 (방향이 같은) r를 eigen-vector라 하고, eigen-value인 L상수만큼 크기는 달라질수 있다.
cov(A)R= RL ==> AR=x
pca에서 cov(A)의 eigen-vector로 이루어진 행렬을 rotation M이라고 하고, eigen-value는 각 PC의 분산(설명력)을 나타낸다.
원데이터 A에 rotation M을 곱한값은 x로 선형변환된 값을 나타낸다.
(모든 Square M가 eigen-decomposition이 가능하지 않지만), Symmetric M은 항상eigen-decomposition가 가능하고, 그 결과는 Orthogonal M이다.
Identity M(단위행렬)
: Main diagonal이 전부 1이고, off diagonal 는 0을 값을 갖는 정사각행렬
MIT gilbert strang : https://www.youtube.com/watch?v=ZK3O402wf1c
https://twlab.tistory.com/12
http://freshrimpsushi.tistory.com/67
https://wikidocs.net/4049
Matrix Algebra in r : www.statmethods.net/advstats/matrix.html