e, euler’s Number, 자연상수

Published by onesixx on 21-01-0621-01-06

https://youtu.be/_EY8QUKWrhc, https://angeloyeo.github.io/2019/09/04/natural_number_e.html
http://blog.naver.com/somang8991/221473671059

e 정의란?

수익률(성장률, 연이율), 성장횟수, 수익(성장량)

[수익률] 100% 을 가지고, 1회의 [성장횟수] n번 나누어 n회 연속성장 할때, 가질 수 있는 최대 [성장량]

자연상수 \ \ e = \lim_{n \to \infin} (1+\dfrac{1}{n})^n \ \quad \ 또는 = \lim_{n \to 0} (1+n)^\dfrac{1}{n}

\rightarrow {\color{green}연속성장}(1+ \frac{\color{red}수익률}{\color{blue}성장횟수})^{ \color{blue} 성장횟수} = 수익 \\ \\ .\\ \lim_{n \to \infin}{ ( 1 + \frac{1.00 }{n} ) ^ n }= 2.7182... ^1 = e^1 =e \\ .\\ \lim_{n \to \infin}{ ( 1 + \frac{r }{n} ) ^ n }= 2.7182...^r = e^r

복리수익은 이자에 다시 이자가 붙는 방식이므로, 같은 이자율을 적용하더라도, 이자계산을 자주할수록 수익이 더 높아지지만, 최대 e^r 까지만 높아질 수 있다.

성장횟수가 1회인 경우, \\~\\ e^r = 수익 = 성장량 = e^{성장횟수* 수익률} = e^{수익률} \\~\\ e^r = \frac{P_t}{P_{t-1}} = \frac{현재가격}{과거가격} \\~ \\ r=ln(\frac{P_t}{P_{t-1}}) \\~\\ r은 \ 수익률, 특히 \ 로그수익률

A = e^{성장횟수* 수익률} = e^r = 성장량 = e^{수익률} \\~\\ A라는 \ 성장량을 \ 알고 \ 있다면, \\~\\ ln e^{성장횟수*수익률} = 성장횟수* 수익률 \\~ \\ 자연로그 \ ln을 \ 활용해서 \ 성장횟수*성장률을 \ 계산할 \ 수 \ 있다.

m회\ 연속성장: \\~\\ 연속성장 \ 2회 \ 일때, \ \ e^2 \ \ \ \ \ \ \ \ 연속성장 \ m회 \ 일때, \ \ \ e^m \\~\\ 성장률\ y = e^{mr} =e^m = e^r 일때: \\~\\ 성장률 \ 50\% \ 이면, \ \ e^{0.5} \ \ \ \ \ \ \ \ 성장률 \ 200\% \ 이면, \ \ \ e^2

e 수학적 정의

https://youtu.be/4w2X9LqvIHc

e=\lim_{n\rightarrow\infin}(1+\frac{1}{n})^n \qquad\qquad e=\sum^\infin_{n=0}\frac{1}{n} \qquad \qquad \int^e_1\frac{1}{x}dx = 1 \qquad\qquad 2.7182818...

아무리 미분해도, 자기자신이 된다.

y=e^x \rightarrow y^\prime= e^x \rightarrow y^{\prime\prime}= e^x \qquad\qquad y=log_ex \rightarrow y^\prime= \frac{1}{x} \qquad\qquad ...

e 정의 : 1회 연속성장(lim)시

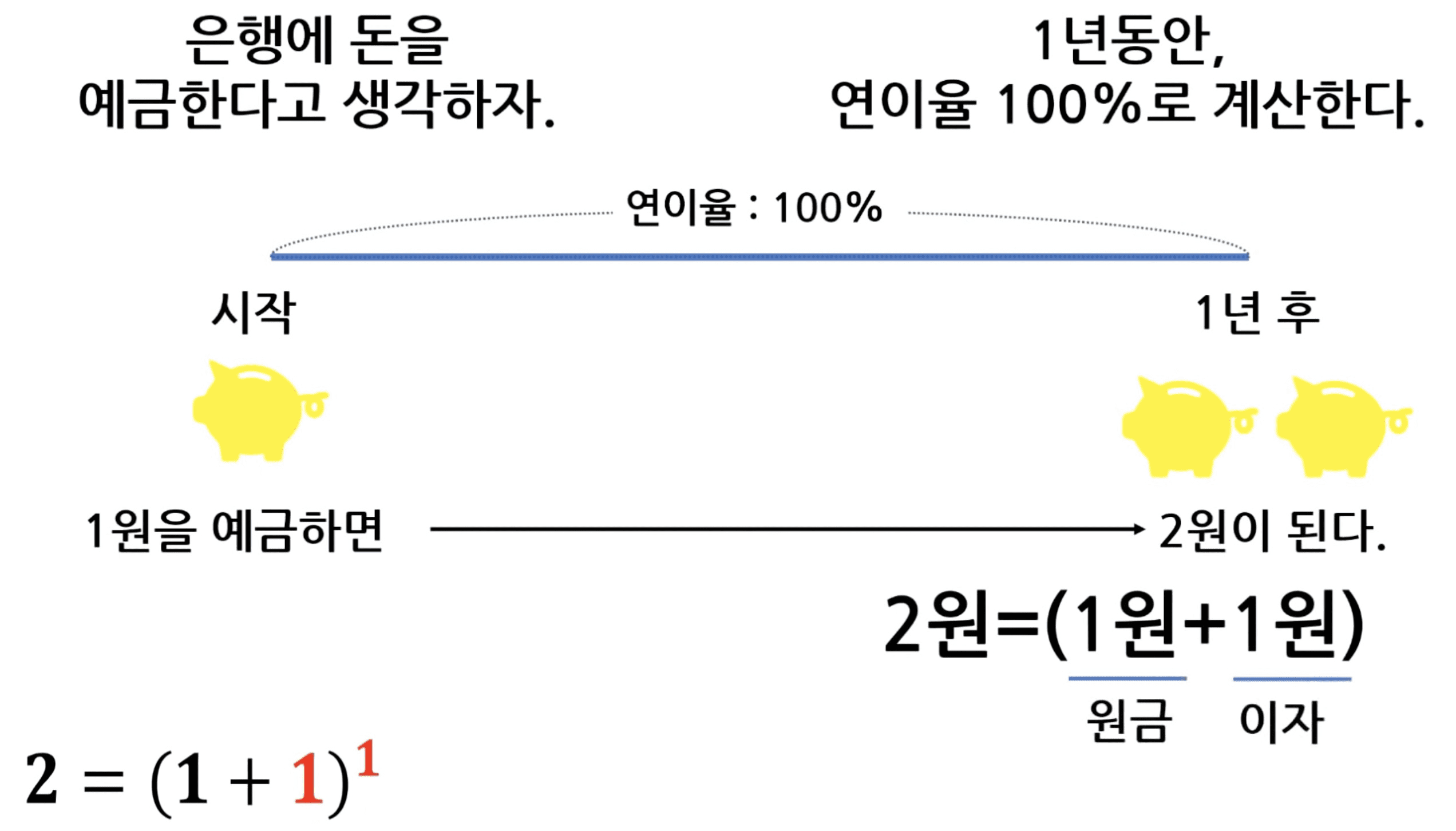
[수익률](연이율) 100% 을 가지고, 1회[성장횟수]를 n회나누어 계속 연속성장 할때, 가질 수 있는 최대 [성장량]

자연의 연속한 성장(growth)을 표현
: 나무가 자라는 속도는 처음에는 크게 자라는 것 같지만, 결국 성장속도는 더뎌지고, 한계가 있다.
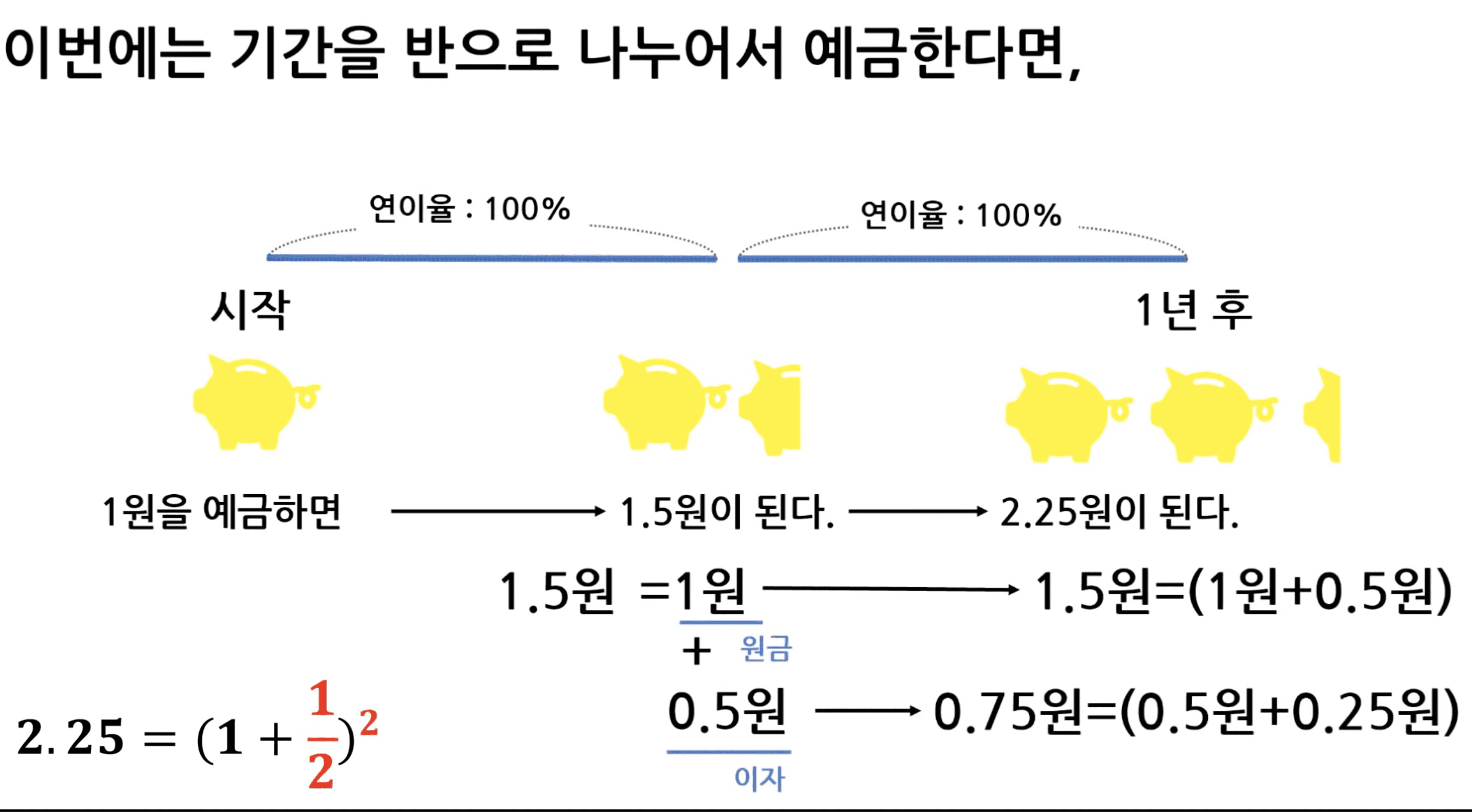
cf. 파이(3.14…)을 통해 모든 원의 둘레 넓이를 표현할수 있는 비율상수.
정해진 연이자율(10%) 을 기간별로 나눠받기
: 10%의 이자율을 1~100까지 나눠받으면, 이자가 어는정도의 액수이상 커지지 않느다.

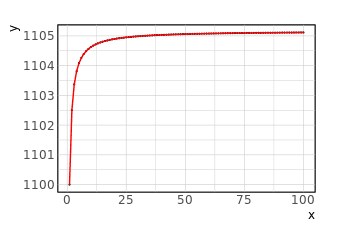
n <- seq(0, 1, by=.01)  # 1:100
#원금 1000원, 연이자율 10%, 1번부터 100번까지.
y= 1000 * (1 + (0.1/n))^n
data.table(x=n, y) %>% ggplot(aes(x,y)) + 
  geom_point(size=.6) + geom_path(color="red")

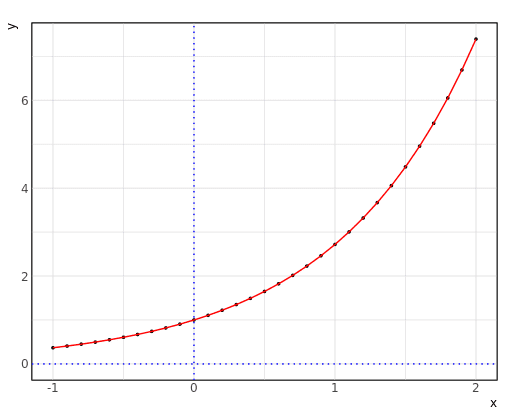
결과적으로 e ^ (성장률, 성장횟수) 에 따라 달라짐

n <- seq(-1, 2, by=.1)
y=exp(n)  # 2.718^n

data.table(x=n, y) %>% ggplot(aes(x,y)) + 
  geom_point(size=.6) + geom_path(color="red") + 
  geom_vline(xintercept=0, lty=3, color="blue") + 
  geom_hline(yintercept=0, lty=3, color="blue")