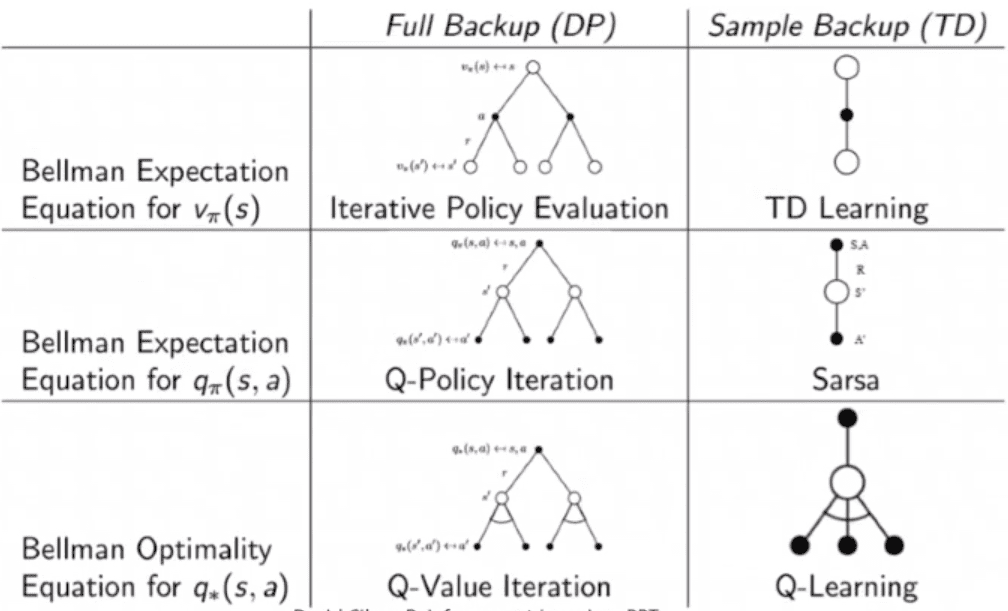
Model-free Prediction & Control
RL이란
1) 일단, 해보고 => 경험
2) 자신을 평가하고 ==> evaluation , prediction
3) 평가한대로 자신을 업데이트 => improve, control
4) 1~3 반복 ==> Iteration
http://www.kocw.net/home/search/kemView.do?kemId=1367683
Model-free Prediction
Monte Carlo Approximation
무작위로 일단 해본다.
그 경험으로부터 얻은 sample을 통해서, True값 추청
sample이 많아지면, True값에 근사.
import random
def estimate_pi(num_samples):
inside_circle = 0
for _ in range(num_samples):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
# 원의 중심으로부터의 거리를 계산
distance = x**2 + y**2
# 원 안에 있는 경우
if distance <= 1:
inside_circle += 1
# 원의 면적을 추정
pi_estimate = (inside_circle / num_samples) * 4
return pi_estimate
# 시뮬레이션에 사용할 샘플 수를 정의
num_samples = 1000000
# 원주율 값을 추정
pi_estimate = estimate_pi(num_samples)
print(f"Monte Carlo 시뮬레이션을 통한 원주율 추정: {pi_estimate}") # 3.143448
샘플링 : Agent가 Environment에서 한번 Episode (= sample ) 를 진행하는것
=> 샘플링을 통해 얻은 Sample의 평균은 참가지함수의 추정값
Policy evaluation에서 [기대값을 계산하지않고], 샘플링을 통해 참가치함수 예측
V?(s) = ??[Gt | St =s]
= ??[Rt+1 + ?∙Rt+2 + ?2∙Rt+3 + ?3∙Rt+4 + ... + ?T-t-1∙RT | St =s]
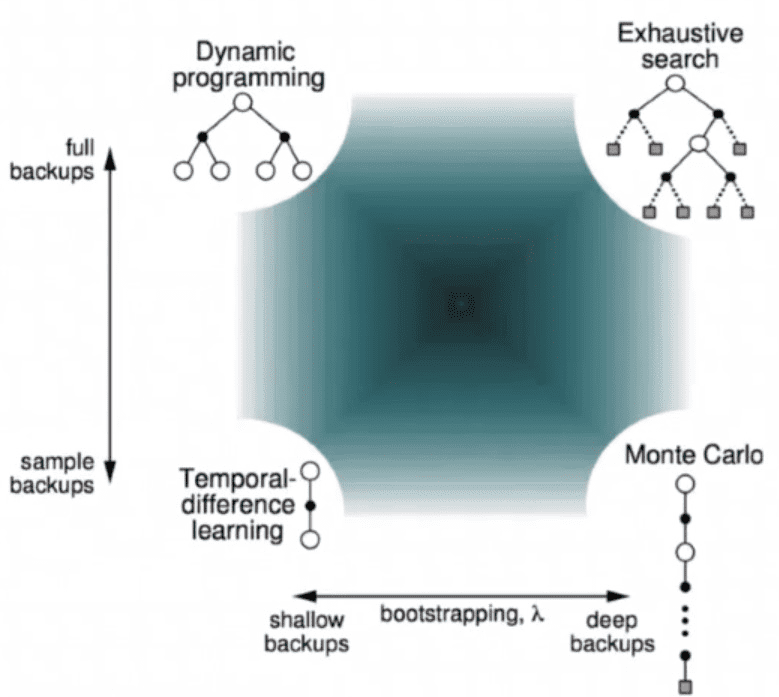
, Temporal Difference
MonteCarlo 예측은 가치함수의 업데이트를 위해, Episode가 끝날때까지 기다려야 함. (실시간이 아님)
=> Episode마다가 아니라, Time Step마다 가치함수 업데이트
Bootstrap : 다른 State의 가치함수 예측값을 통해, 지금 상태의 가치함수를 예측하는 방식'
Gt가 아니라 다음상태 V(St+1)의 예측값만 있으면 된다. 에피소드가 끝나는걸 기다릴 필요없음.

Model-free Control
SARSA : on-Policy
TD(Time difference) Control에서 (가치함수가아닌) Q함수를 업데이트함. ε-greedy로 policy improvement
현재상태은 Q함수(추정값) 를 다음상태의 Q함수(추정값) 로 업데이트
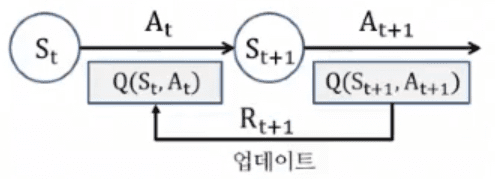
ε-greedy 정책을 통해 [St, At, Rt+1, St+1, At+1] 정책 샘플을 획득하고,
이 샘플을 이용해 Q함수 Q(St, At) 를 업데이트
Q-learning : off-Policy
SALSA에서는 Agent가 ε-greedy로 Action을 하면서 Learning을 한다. (online으로 Action을 하고, online으로 Learning)
=> (자신이 행동하는 대로 학습) Exploration으로 선택한 정책때문에 잘못된 정책을 학습
따라서, Q-Learning은 Action하는 Policy (behavior policy μ, ε-greedy정책) 와
Learning하는 Policy (target policy ?, greedy정책으로 Q함수 업데이트)를 분리
Q함수 업데이트를 위해 [s,a,r,s'] 샘플필요