MDP(Markov Decision Process)
MDP를 해결하기 위한 method들
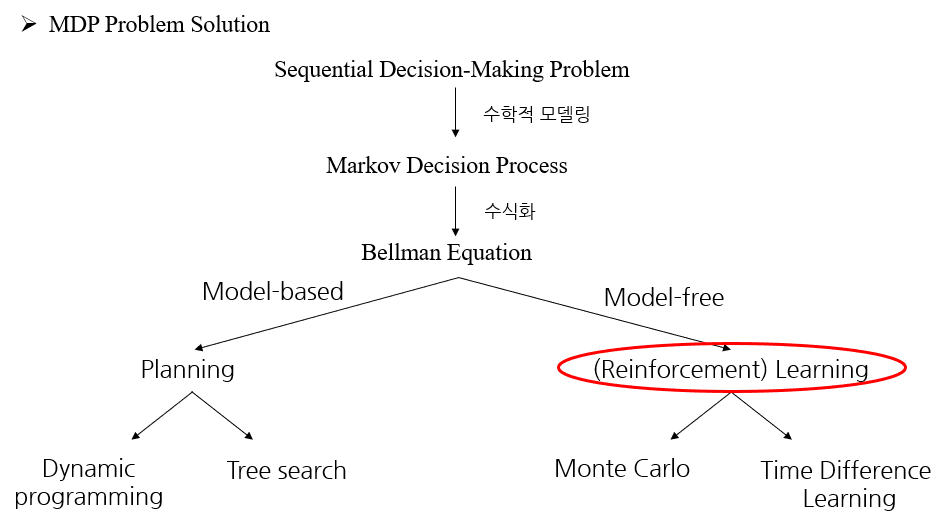
Model-based method
( 모델을 안다 = Agent가 상태변환확률을 알고 있다)
model을 알고 있기 때문에 최적의 수를 planning(계산)가능 => 이리 저리 헤맬 필요 없이 최적의 수를 계산
– Dynamic Programming
(Value Iteration, Policy Iteraction)
– Heuristic search (MCTS: Monte Carlo tree search)
Model-free method
(Agenct가 상태변환확률을 모른다.)
model을 모르기 때문에 이리 저리 헤매며learning(학습), 즉 강화학습을 통해 최적의 수를 찾아간다.
– MonteCarlo method (cf. Monte Carlo 확률계산알고리즘 그 자체)
– TD method
– SARSA, Q-learning…
MDP 를 풀기위한 강화학습
wikibook.co.kr/rlrev/
https://dana-study-log.tistory.com/category/강화학습

상태(S, State)
Agent가 [관찰가능한 상태]의 집합. 대문자 S로 표기
상태를 구체적으로 표현한다면 자신의 “상황에 대한 관찰”이라고 할 수 있다.
Agent가 의사결정을 하기 위해 환경에서 제공해주는 정보를 “가공한” 정보이다.
가공한 정보라고 표현한 이유는 상태는 사용자가 정의하기 나름이기 때문이다.
강화학습은 순차적인 행동결정 문제를 다루기 때문에, 시간정보가 중요하다.
그래서, [t 시간에서의 특정 상태]를 St 라고 표기하며, 소문자 s 로 표시하기도 한다.
이 [특정 시간 t에서의 상태] St는 확률변수이다. 왜냐면, 상태가 시간에 따라 확률적으로 변하는 값이기 때문
즉, St 는 시간 t에 전체 상태 중(위의 예시에선 36가지 상태 중) 하나의 값을 가지고 있다는 뜻이다.
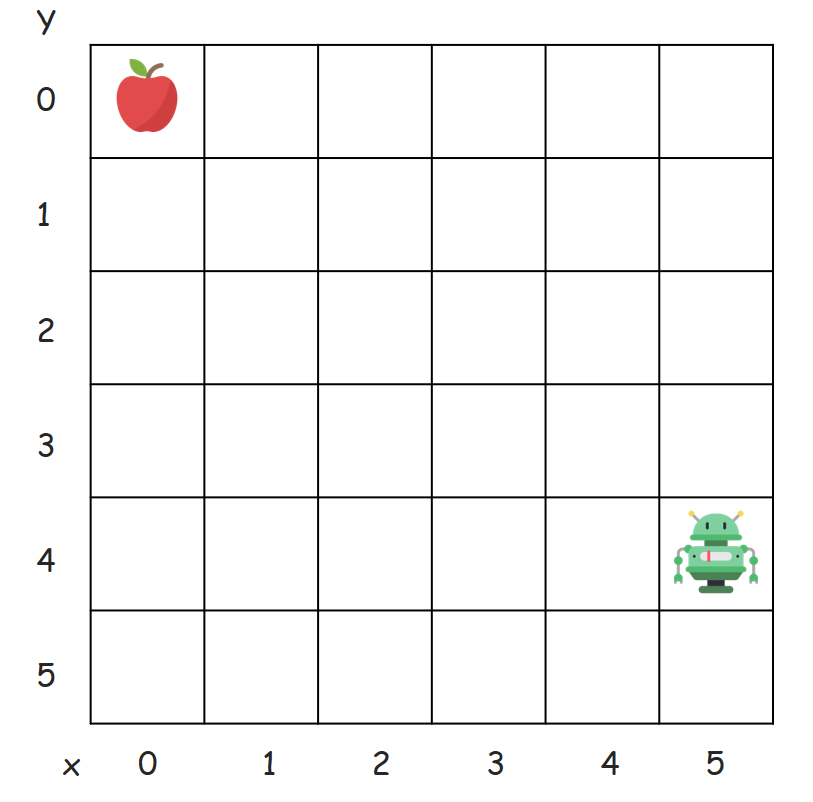
예) 아래 환경(Grid-World)에서
s[상태]를 Grid상의 각 위치정보(x좌표, y좌표)라 정한다면,
S(상태의 집합)은 36가지(6*6)가 될 것이다.
Episode
처음 State부터 마지막 State까지의 sequence
행동(A, Action)
Agent가 의사결정을 통해 취할 수 있는 행동의 집합, 대문자 A로 표기
위의 환경인 Grid-world에서는 상/하/좌/우로 이동하는 것을 말한다.
(대각선으로 이동하는 것까지 포함한다고 정의하면 8가지의 행동이 있는 것이다.)
상태와 마찬가지로, 시간 t에서의 특정 행동은 At = a 이라고 표기한다.
At 또한 시간 t에서 어떤 행동을 할지 정해져 있는 것이 아니므로, 확률변수이다.
시간 t에서 취한 Action의 집합이 Policy
상태 변환(변이) 확률
[상태 s]에서 [행동 a]를 했을 때, [다음 상태 s’]이 될 확률
Environment가 알려주는 변환 확률은 “환경의 모델”이라고도 하며 아래 그림처럼 표기한다.
- 상태변환확률을 안다면 : model-based -> Dynamic Programming
- 상태변환확률을 모른다면: model-free -> Reinforcement Learning
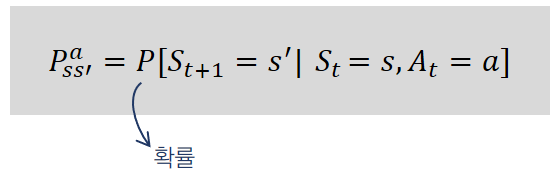
여기서, s’ = St+1 이다.
즉 s’은
[시간 t]에서의 [특정 상태 s]에서 [어떤 행동]을 했을 때, [다음시간 t+1시점]에서의 [특정상태]를 표현한 것이다.
이는 특정 행동을 하면 예상한 다음 상태가 되는 것이 당연하다고 생각해서 그런 것이다. 하지만 특정 상태에서 어떤 행동을 취했다고 꼭 선택한 상태에 도달하는 것은 아니다.
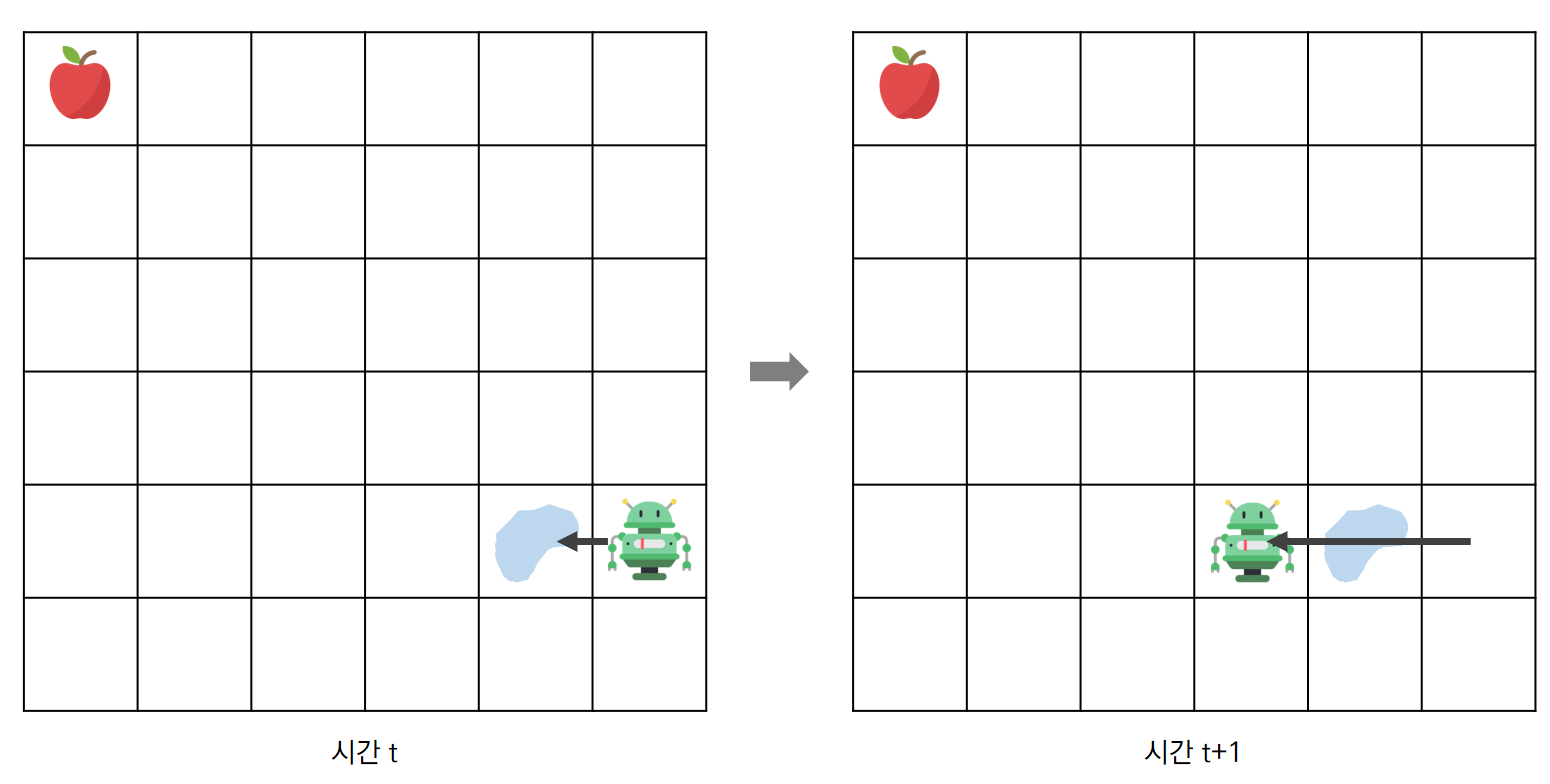
예를들어, Grid-world에서, Agent(로봇)가 현재 위치에서 왼쪽으로 가는 행동을 취했다고 가정하자.
이 때 로봇은 한칸 옆으로 이동하고자 했겠지만 하필 빙판길이 있어서 왼쪽으로 두칸 이동하게 되었다.
이러한 상황이 있을 수 있기 때문에 상태 변환 확률도 고려해야하는 것이다.
위 예시를 수치화해보자면 빙판길에 의해 원하는 곳으로 못갈 확률이 20%라고 했을 때,
로봇이 왼쪽으로 가는 행동을 선택해 원하는 상태로 이동할 상태변환확률은 0.8인 것이다.
보상(R, Reward) => sparse , delayed
Agent가 학습할 수 있는 정보, 대문자 R로 표시.
Agnet가 한 Action에 대한 Environment의 피드백을 말한다.
시간 t에서 받은 보상은 Rt 이라고 표현하며, 역시 특정 값이 정해지지 않았기 때문에 확률변수이다.
주의해야할 점은 보상은 다음 시점에서 받는다.
시간 t에서 어떠한 행동을 선택했다면 상태는 St+1가 되고 St+1상태에서 보상 Rt+1이 주어진다.
*보상함수
현재상태 s에서 행동 a를 통해 얻을 수 있는 보상 Rt+1의 기댓값을 말한다.
(여기서 상태와 행동을 “특정”상태와 “특정”행동을 말하는 것이므로, 소문자 s, a라고 표기했음을 주의해야한다.)
보상함수는 R에 아래첨자 s, 윗첨자 a를 쓰거나 r(s,a) 라고 표현한다.
보상함수는 보상에 대한 기댓값이라고 했는데,기댓값이란 어떤 확률적 사건에 대한 평균의 의미로 생각하면 된다.
수식으로 표현하면 아래와 같이 표현할 수 있다.
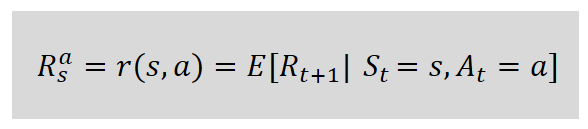
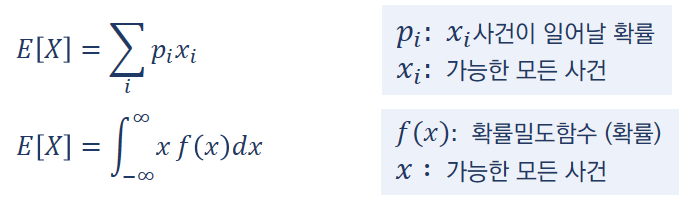
예시로 주사위 눈의 수에 대한 기댓값을 구해보자면 (1/6) + (2/6) + (3/6) + (4/6) + (5/6) + (6/6) = 3.5이다.
이 기대값의 의미를 생각해보면 주사위를 던졌을 때 나오는 눈의 값은 평균적으로 3.5 라는 뜻이다.
즉, 기댓값은 ‘나오게 될 숫자에 대한 예상’이라고 할 수 있다.
반환값 (G) with 감가율(?)
각 상태에서의 가치를 판단하기 위해서 가치함수내의 반환값을 사용한다.
반환값은 (단순히 각 상태에서 보상들을 합이 아닌) [시간 t 이후 상태들]에서 감가율을 적용한 [보상]들의 합을 말한다.
미래에 받을 R을 현재의 시점에서 고려할 때 감가하는 비율.
감가율은 0에서 1사이의 값이며, 반영의 비중을 조절하기 위해 감가율을 조정할 수 있고,
초기 상태에서 효율적인 행동을 선택하기 위해서, 미래의 정보를 반영하는 것이다.
반환값을 구할때, 감가율을 적용하는 이유
- 현재 받는 보상과 미래에 받는 보상을 구분하지 못한다.
t 시점에서 100의 보상을 받는 것이나, 후에 100의 보상을 받는 것이나 단순 보상의 합으로는 똑같이 100이기 때문에 시점을 구분할 수 없게 된다. 그렇게 되면 현재 이익이 큰 상태로 가는 행동을 취할 수 없게 된다. - 한 번에 받는 보상과 여러 번 나눠서 받는 보상을 구분하지 못한다.
20의 보상을 5번 나누어 받는 것과 한번에 100을 받는 것을 구분하지 못할 것이다. - 시간이 무한대일 경우 보상의 합을 수치적으로 구분할 수 없다.
0.1의 보상씩 받는 경우와 10씩 보상을 받는 경우는 시간이 무한대가 되면 구분할 수 없다.
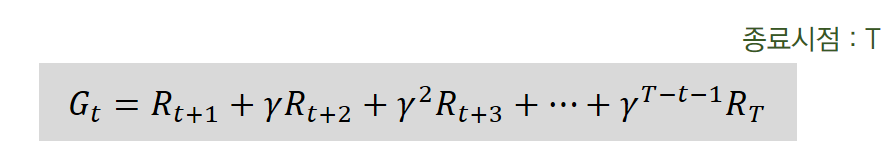
반환값을 이용해서, 상태의 가치를 판단하는지 방법은 가치함수 부분을 공부하면 알게 될 것이다.
반환값은 Gt 라고 표기하며, 확률변수의 보상들의 합이 반환값이므로 반환값도 확률변수이다.
즉, Episode마다 행동과 상태도 확률적으로 달라지고 따라서 보상도 달라지기 때문에 반환값 역시 변할 수 있다.
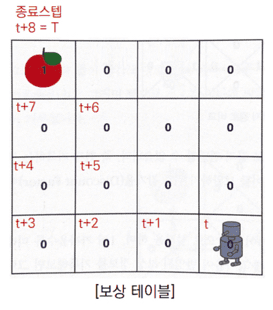
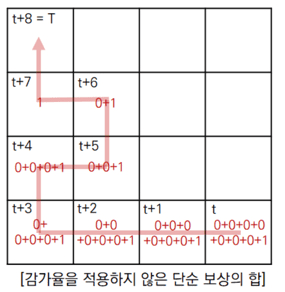
보상테이블을 기반으로, 감가율을 적용하여 반환값을 각 상태에서 구한 것이다.
보상은 사과에 도착했을 때만 1이 주어지고 나머지 상태에선 0이다.
위의 반환값을 구하는 과정은 빨간색 경로에 대해서만 나타낸 것이다.
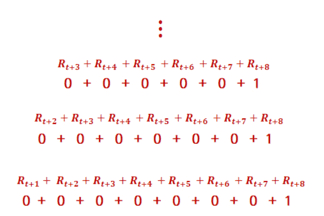

[{0, 1.0}, {0.9, 1}, {0.81, 2}, {0.729, 3}, {0.656, 4}, {0.59, 5}, {0.531, 6}]
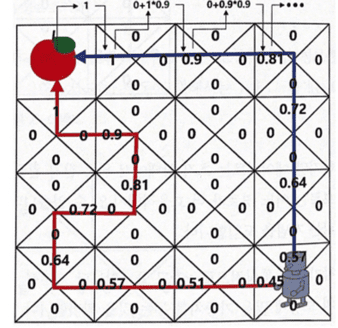
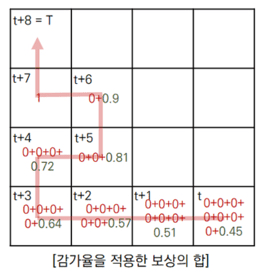
결론적으로 제일 마지막 [감가율을 적용한 보상의 합]을 보면,
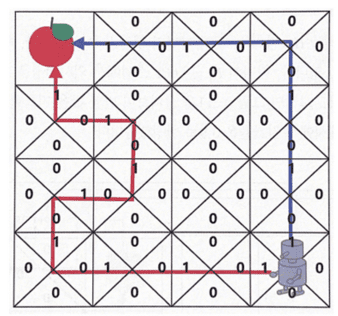
빨간색 경로와 파란색 경로에 대해서 지나간 모든 상태에서 반환값을 감가율을 적용해 구한 것이 표시되어 있는데,
단순 보상의 합의 표와 비교했을 때 당장 로봇의 위치에서 위로(파란색 경로) 가는 행동을 취하는 것이 더욱 효율적인 경로를 선택한 것임을 확인할 수 있다.
위의 (방법은 가치함수가 아닌) 단순히 반환값으로만 경로를 선택한 것이다. (감가율의 효능을 보이기 위함)
Policy 정책
Agent는 각 State마다 (단 하나의) Action을 선택하게 되는데… 이것을 확률로 나타낸것
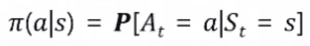
각 State에서 어떤Action을 할지에 대한 정보 => Policy
그 중 “최적 Policy”는 Agent가 강화학습을 통해 학습해야 할 목표, Stochatic Policy -> Deterministic Policy
(상태) 가치함수 : value of state function
RL에서 Reward는 학습의 기준이 되고, Reward의 합이 큰쪽으로 Action을 선택하게 된다.
하지만 특정 시점에서 아직 받지 않은 Reward(보상은 행동을 취한 뒤 다음 상태에서 받음) 들을 어떻게 고려해야 할까?
이에 대한 개념이 가치함수이다. MDP => Value Function => Action선택
즉, 가치함수가 특정 상태에 대한 ‘가치’를 계산해주어, Agent가 Action을 선택할 수 있도록 도와주는 것이다.
가치함수란?
특정 State서의 Return반환값들, 상태의 가치를 판단한다고 해서 ‘상태 가치함수’라 한다.
[시간 t 이후 상태들]에서 (감가율을 통해 할인을 적용한) 반환값 G의 “기댓값“
현재 상태의 가치는 [현재 특정 상태]에서, 한 에피소드가 끝날 때까지(행동의 선택들이 끝나 마지막 지점에 이를 때까지) 받은 보상들의 합을 통해 판단할 수 있다.

예) grid world에서 현재 상태에서 오른쪽으로 가는 경로(ex. →→↑)와 왼쪽으로 가는 경로(ex. ←↑→→→) 중에 고민을 하고 있다고 가정하자.
두 경로로 가는 행동들을 끝내고(에피소드가 끝나고) 받은 보상들의 값이 더욱 큰 쪽으로 가는게 효율적인 선택이라고 판단할 수 있다. 그래서 가치함수의 개념에 보상의 합을 이용하는 것이다. 하지만 보상들의 단순 합으로 상태의 가치를 판단하기엔 시간 개념을 적용할 수 없다. 따라서 보상의 단순 합에 감가율을 적용한 반환값을 이용한다!
또한, 반환값은 보상 자체가 확률변수이기 때문에 (상태와 행동에 따라 변하므로) 반환값 또한 확률변수이다.
따라서 평균의 의미인 기댓값을 반환값에 적용하는 것이다.
Agent가 갈수 있는 State들의 가치를 안다면, 그 중 가치가 가장 높은 State를 선택할수 있음.
즉 기대값을 계산하기 위해서는 환경의 모델을 알아야함.
– Dynamic Programming으로 가치함수 계산
– 가치함수를 계산하지 않고, RL은 sampling을 통해 추정
행동 가치함수 : Q함수 : Quality of action function
상태 가치함수를 통해 다음 상태들의 가치를 판단할 수 있고,
이를 바탕으로, 더 높은 가치를 가지고 있는 다음 상태로 가기 위한 Action을 선택하여 상태를 이동시킬 것이다.
하지만 그러기 위해선 [다음 상태]들에 대한 정보를 모두 알아야 하고, 그 상태로 가기 위한 행동을 선택하더라도 “상태 변환확률”도 고려해야 한다. (Agent는 가치가 더 높은 특정 다음 상태로 이동하려 했는데, 어떠한 확률로 그 상태로 이동하지 못할 수도 있으니)
따라서 (상태)가치함수말고, 행동에 대한 가치함수를 구할 수 있어야 하는데, 이러한 개념이 Q함수이다.
Q함수를 이용하면 행동에 대한 가치함수 값을 보고 어떤 행동을 할지 판단하면 되기 때문에, 상태들의 가치를 판단하고 어떤 행동을 했을 때 특정 다음 상태로 가게 될 확률도 고려해야 하는 번거로움이 없어진다. 즉, Q함수는 특정 상태 s에서 특정 행동 a를 취했을 때 받을 반환값에 대한 기댓값으로 특정 행동 a를 했을 때 얼마나 좋을 것인지에 대한 값이다.
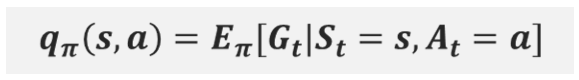
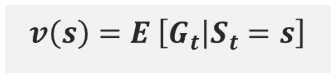
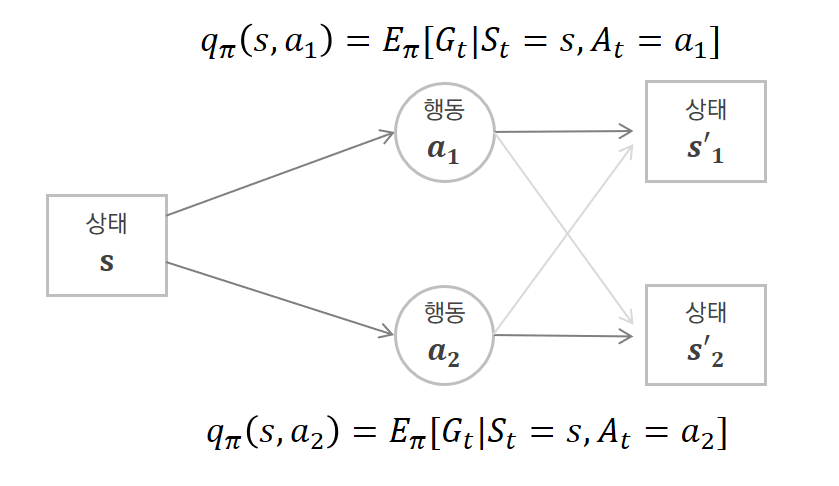
위의 그림으로 상태 가치함수와 행동 가치함수를 비교해보자.
상태 s에서 할 수 있는 행동이 a1과 a2로 두 가지 있다고 가정한다. 또한 상태 s에서 행동을 취했을 때 갈 수 있는 다음 상태 s’이 s’1과 s’2가 있다.
상태s의 상태 가치함수는 행동 a1을 취한 이후에 받는 반환값들과 행동 a2를 취한 이후에 받는 반환값들을 모두 고려해서 기댓값을 구한 것이다.
행동 가치함수는 상태 s에서의 행동 가치함수는 2가지가 나올 것이다. (취할 수 있는 행동이 2개이기 때문에) 한 가지 Q함수는 행동 a1을 취한 이후에 받는 반환값들에 대해서만 기댓값을 구한 것이고, 나머지 Q함수는 행동 a2를 취한 이후에 받는 반환값들에 대해서만 기댓값을 구한 것이다.
여기서 단일 에피소드만 고려한다고 했을 때, 특정 상태에서 특정 행동을 선택하여 에피소드를 진행했는데 반환값들이라고 복수로 표현한 이유는 두 가지가 있다.
– 첫 번째는 그림에서도 표현되어있듯이 행동 a1을 선택하면 상태 s’1으로 갈 것이라고 예상하여도
상태 변환 확률로 인해 상태 s’2로 갈 확률이 있기 때문에, 두 경우의 반환값의 기댓값을 구해야 한다.
– 두 번째는 상태 변환 확률이 1이어서 행동 a1을 취하면 무조건 상태 s’1으로 이동한다고 가정해도,
상태 s에서의 반환값은 상태 s’1에서 즉시 받는 보상과 s’1에서의 가치함수에 감가율을 적용한 것의 합이기 때문에 기댓값 개념이 포함된다. (s’1에서의 가치함수에 기댓값 개념 포함) <== 벨만 기대 방정식을 참고
상태 가치함수와 행동 가치함수의 관계
각 행동을 했을 때의 가치인 “Q함수”에 그 행동이 일어날 확률을 곱해서
모든 행동에 대해 그 값을 더해주면 “상태 가치함수”가 된다.
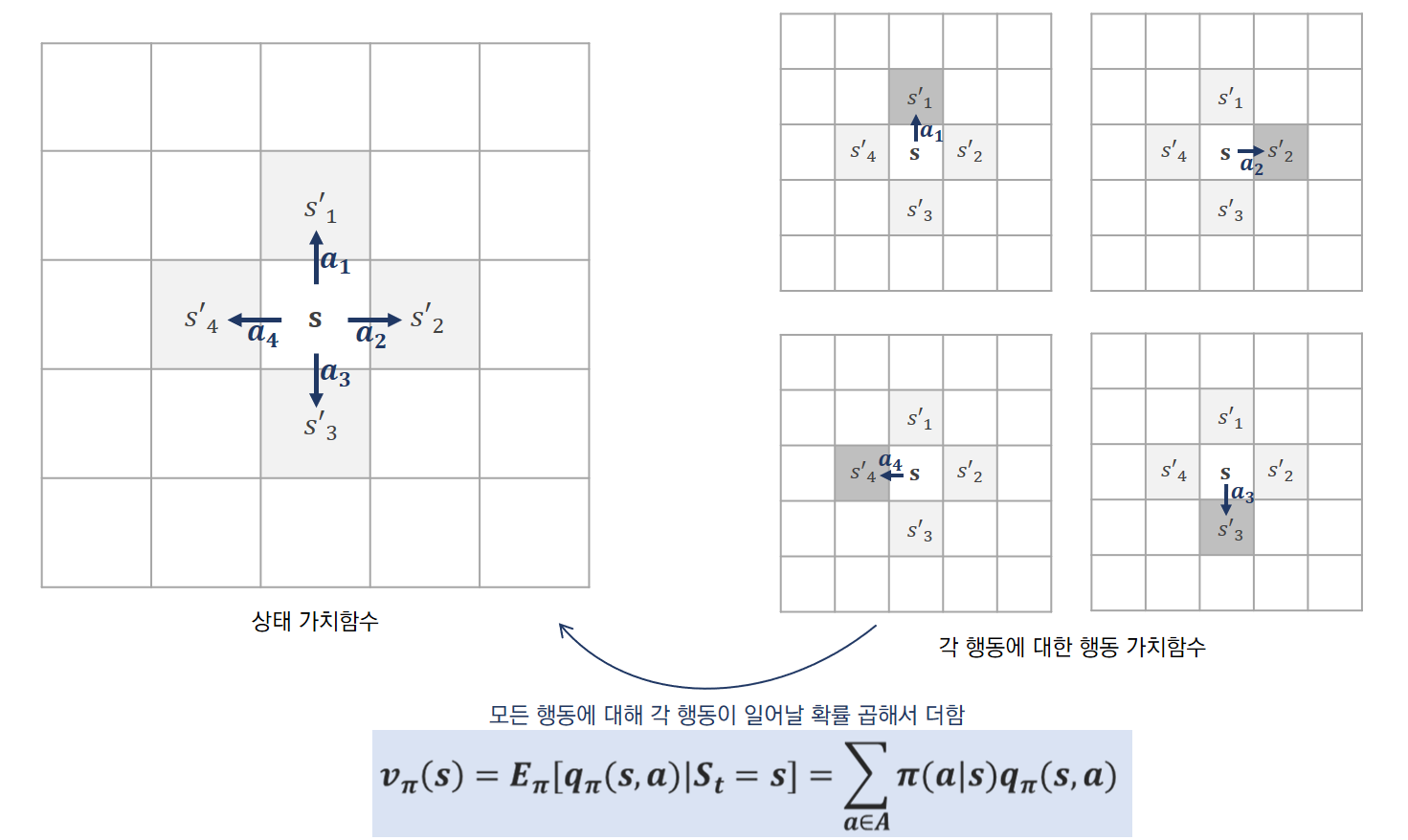
위의 예에서, 오른쪽은 각 행동에 대한 Q함수(행동가치함수)를 표현했는데, 상태 s에서 할 수 있는 행동은 a1~a4로 상우하좌로 이동하려는 행동이다. 그림에서 진한 회색은 상태 s에서 각 행동을 했을 때 제대로 이동한 다음 상태이고 연한 회색은 상태 변환 확률로 인해 적은 확률로 다른 상태로 이동할 가능성을 나타낸 것이다.
위의 환경에서 만약 상하좌우로 이동하는 행동의 확률이 동일하다면 각 행동이 일어날 확률은 1/4이다. 4가지 경우의 행동 모두에 대해 1/4 확률과 각 행동에 대한 Q함수를 곱한 후 이 값을 모두 더해지면 상태 s에서의 상태 가치함수와 같은 값이 나온다.