FAQ: HOW DO I INTERPRET ODDS RATIOS IN LOGISTIC REGRESSION?

http://kkokkilkon.tistory.com/19

 

Intro.

logistic regression을 사용하여, “Binary outcome variable(Y, 이진 범주형 변수)”를 모델링할때, 
Y의 logit변형값은  X와 선형관계를 가진다는 가정을 한다.  따라서 coefficient 해석에 주의를 기울일 필요가 있다.    …odds ratio…

P         =   β0 + X β1	Linear regression의 Y는 예측하고자 하는 값	0 =<        P            =<  1
P/(1-P)     =   β0 + X β1	Logistic regression에서, Y 는 어떤 Category에 속할 확률 odds =  속할 확률/ 속하지않을 확률  =  성공확률/  실패확률   = P / (1-P)	0 =<    P/(1-P)    =<  inf.
ln (P/(1-P))   =   β0 + X β1	Log odds	– inf. =< ln (P/(1-P))=<inf.

 

odds의 확률부터 Odds의 log까지 

성공의 odds는 실패확률에 대한 성공확률의 비율.

어떤 event의 성공 확률은 80%, 실패확률은 당연히 20%라고 할때,  성공의 odds는  80%/20% = 4.  ( 실패의 odds를 1로 )
어떤 event의 성공확률이 50%라고 하면, 성공의 Odds는 1이고, 실패의 Odds도 1이다. 

Y의 값은 분류를 위한 확률값 P이다. 

좌우변의 범위(-inf~inf)를 일치하기 위해 logit을 대입하여, 최소제곱법을 적용한다. 

P에 관해 정리하면, 
e를 씌움 =>  ,   역수를  취해 정리  ==> , 
1을 더함 ==> , 역수를 취해 정리 

 

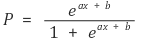
단조 로그 변환 monotonic/log transformation

확률이 증가하면 Odds도 증가하므로, 확률에서 Odds로의 변환은 단조변환이라 할수 있다.  물론 역도 성립한다.
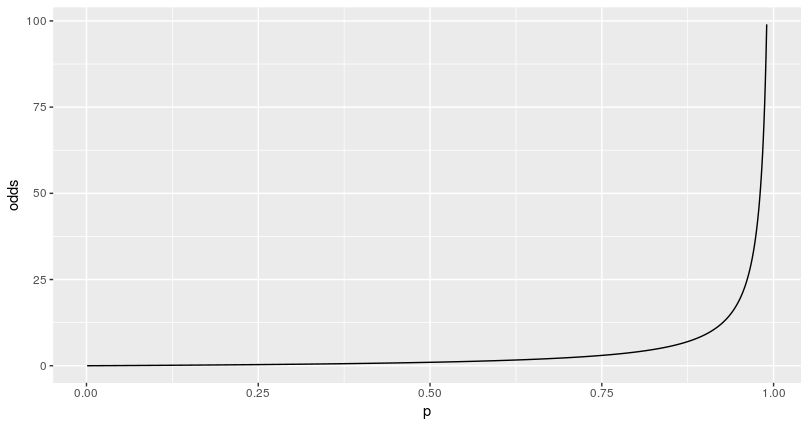
다만, 확률은 0과 1사이의 값이지만, Odds는 0부터 양의 무한대의 범위를 가진다. 

p        <- seq(0,.99,by=0.001)
odds     <- p/(1-p)
log_odds <- log(odds)
df <- as.data.frame(cbind(p,odds,log_odds))[-1,]

ggplot(df) + geom_line(aes(p,odds))
ggplot(df) + geom_line(aes(p,log_odds))

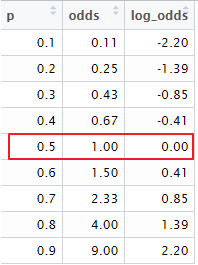
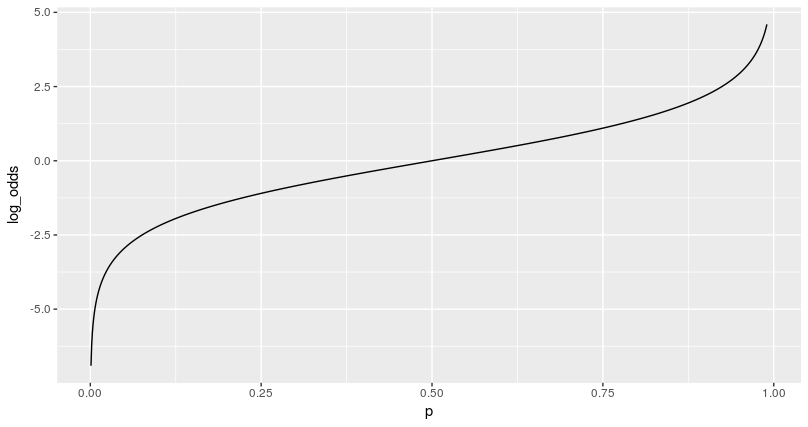
왜 굳이 확률을 log odds로 변환해야하나?

1. 확률처럼 범위가 제한된 변수를 일반적으로 modeling하기 어렵다.
2. odds의 log변환 (logit transformation)은 다른 변환에 비해 이해하고 해석하기 쉽다.  (cf. probit transformation)

최적의 임계치는?

임계치를 기준으로 작으면 0, 크면 1로 분류 한다. 이때 임계치는 Validation Set의 분류 정확도에 따라 결정한다.