Markov chain

Markov chain

https://youtu.be/Yh62wN2kMkA : Markov chain

a stochastic process that undergoes transitions from one state to another based on certain probabilistic rules.

이산적 시간의 흐름에 따라, (바로 전 시간t의 state 또는 event 에만 영향을 받는)
어떤 state / event가 발생할 확률값이 변화해 가는 과정
=> 그 확률값은 수렴해간다.

마르코프연쇄를 따르는 State에, Action과 Reward를 추가한 확률과정 => Reinforce learning!

마르코프 가정

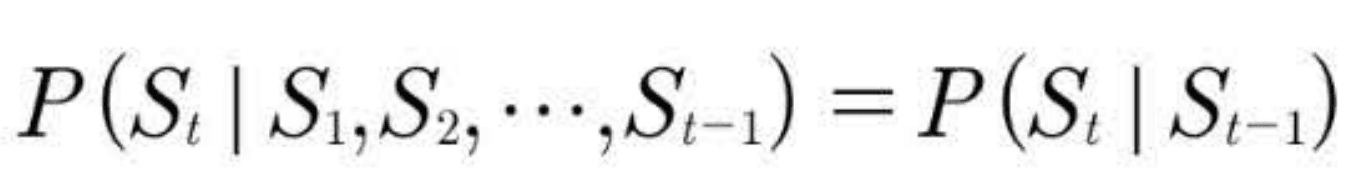
Markov Chain과 MDP는 근본적으로 다르다

Markov Chain ~> MP(Markov Process) -> MRP (+Reward) -> MDP ( +Action : Policy)

강화학습은 MDP에 학습의 개념을 넣은것

MP

Markov가정을 만족하는 연속적인 일련의 상태

• 일련의 상태 < S₁, S₂, …, Sₜ>
• State Transition Probability <P>

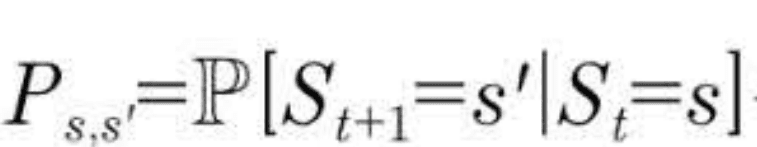
MDP (Markov Decision Process)

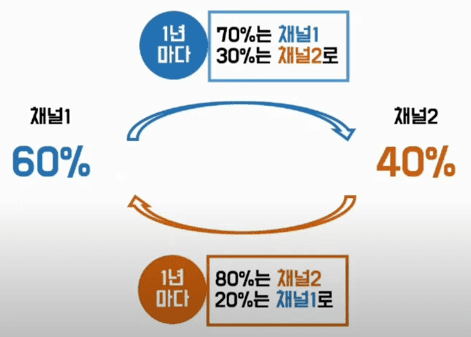
2023년 시청률은 2022년 시청률을 기반으로 계산됨

각 방송국 시청률에 대한 현재 State 는 MBC 60% , KBS 40% => X(t=0) = [ 0.6, 0.4 ]

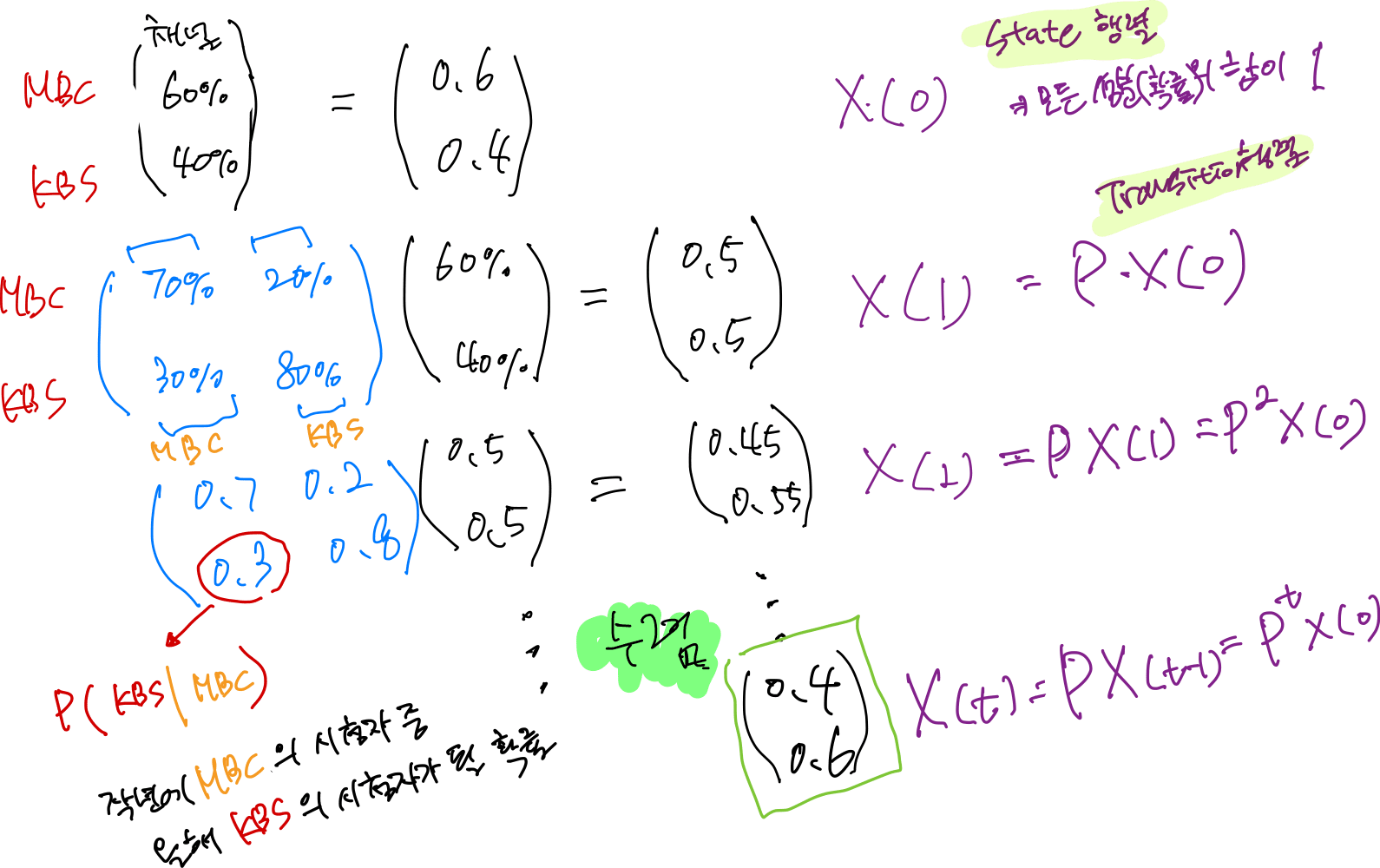
import numpy as np

# Initial state probabilities X(t=0)
initial_state  = np.array([0.6, 0.4])

# Define the transition matrix
# Each row represents the probabilities of transitioning to other states
transition_matrix = np.array([[0.7, 0.3], [0.2, 0.8]])

# Way1:
current_state = initial_state
num_steps = 0
while True:
    print(f"t={num_steps}th, Current state:{current_state}")
    next_state = np.dot(transition_matrix, current_state)
    if np.array_equal(current_state, next_state):
        break
    num_steps += 1
    current_state = next_state

t=0th, Current state:[0.6 0.4]
t=1th, Current state:[0.54 0.44]
t=2th, Current state:[0.51 0.46]
t=3th, Current state:[0.495 0.47 ]
t=4th, Current state:[0.4875 0.475 ]
t=5th, Current state:[0.48375 0.4775 ]
t=6th, Current state:[0.481875 0.47875 ]
t=7th, Current state:[0.4809375 0.479375 ]
t=8th, Current state:[0.48046875 0.4796875 ]
t=9th, Current state:[0.48023437 0.47984375]
t=10th, Current state:[0.48011719 0.47992188]
t=11th, Current state:[0.48005859 0.47996094]
t=12th, Current state:[0.4800293  0.47998047]
t=13th, Current state:[0.48001465 0.47999023]
t=14th, Current state:[0.48000732 0.47999512]
t=15th, Current state:[0.48000366 0.47999756]
t=16th, Current state:[0.48000183 0.47999878]
t=17th, Current state:[0.48000092 0.47999939]
t=18th, Current state:[0.48000046 0.47999969]
t=19th, Current state:[0.48000023 0.47999985]
t=20th, Current state:[0.48000011 0.47999992]
t=21th, Current state:[0.48000006 0.47999996]
t=22th, Current state:[0.48000003 0.47999998]
t=23th, Current state:[0.48000001 0.47999999]
t=24th, Current state:[0.48000001 0.48      ]
...
t=49th, Current state:[0.48 0.48]
t=50th, Current state:[0.48 0.48]
t=51th, Current state:[0.48 0.48]
t=52th, Current state:[0.48 0.48]

# Way2:
num_steps = 0
current_state = initial_state
P = transition_matrix
while True:
    print(f"t={num_steps}th, Current state:{current_state}")
    next_state =  P @ initial_state
    P =  P @ transition_matrix
    if np.array_equal(current_state, next_state):
        break
    num_steps += 1
    current_state = next_state

# Way3: diagonalization
# 대각화 가능한 행렬
A = transition_matrix

# 고유값과 고유벡터 계산
eigenvalues, eigenvectors = np.linalg.eig(transition_matrix)
# 대각화
D = np.diag(eigenvalues)  # 대각행렬
Q = eigenvectors          # 고유벡터 행렬

# 유사 대각행렬로 변환
# similar_diag = np.linalg.inv(Q) @ A @ Q
np.linalg.inv(Q) @ D @ Q

for i in range(60):
    P = np.linalg.inv(Q) @ np.linalg.matrix_power(D, i) @ Q
    C = P @ initial_state
    print(f"t={i}th, Current state:{C}")

import numpy as np

# Initial state probabilities X(t=0)
initial_state  = np.array([0.153, 0.142, 0.141, 0.141, 0.141, 0.141, 0.141])

# Define the transition matrix
# Each row represents the probabilities of transitioning to other states
transition_matrix = np.array([  [  0,   0,   0, 0.1,  0, 0.2, 0], 
                                [0.5,   0,   0,   0,  0, 0.4, 0],
                                [  0, 0.8,   0,   0,  0, 0.4, 0],
                                [0.5,   0,   0, 0.9,  0,   0, 0],
                                [  0,   0, 0.6,   0,  0,   0, 0],
                                [  0,   0, 0.4,   0,  0,   0, 0],
                                [  0, 0.2,   0,   0,  1,   0, 1]
                            ])  

# Way1:
num_steps = 0
current_state = initial_state
while True:
    print(f"t={num_steps}th, Current state:{current_state}")
    # next_state = np.dot(transition_matrix, current_state)
    next_state = transition_matrix @ current_state
    if np.array_equal(current_state, next_state):
        break
    num_steps += 1
    current_state = next_state

print(f"t={num_steps}th, Current state:{np.around(current_state, decimals=2)}")

MRP ( Markov Reward Process )

S, P, R, r가 주어진다면 => Markov Reward Process

cf) S, P가 주어진다면 => Markov Process가 정의

Reward Process에는 Action이란 게 없습니다.
단지, 확률에 따른 state가 정해지기 때문에 action이 아닌 state에만 reward가 주어지면 되는 것입니다. (즉각적인 Reward)
MDP에서는 State뿐만아니라 Action에도 Reward가 주어짐.

Env모델 = State Transition 모델 + Reward 모델

MDP  매 스텝마다 받는 Reward의 누적 Reward이 최대화

= return, value 함수