ISLR :: 5.2 The Bootstrap
5.2 The Bootstrap
bootstrap은 learning method 또는 주어진 추정량(estimator)과 관련된 불확실성을 수량화하는데 사용될 수 있는
아주 강력하면서도 널리 사용되는 통계적 tool이다.
간단한 예로, bootstrap은 linear regression fit에서 구한 coefficient의 standard errors를 추정하는데 사용될 수 있다.
(사실 linear regression 경우에는 R에서 표준오차와 같은 결과를 제공해주기 때문에 유용하지 않을 수 있지만,
bootstrap의 강점은 R에서 제공하지 않거나 변동성의 측정이 어려운 learning method에 광범위하게 적용될 수 있다. )
모집단으로부터 독립적인 data-set들을 반복적으로 얻는 대신에,
original data-set으로부터 반복적으로 관측치를 sampling하여 별개의 data-set을 얻는다.
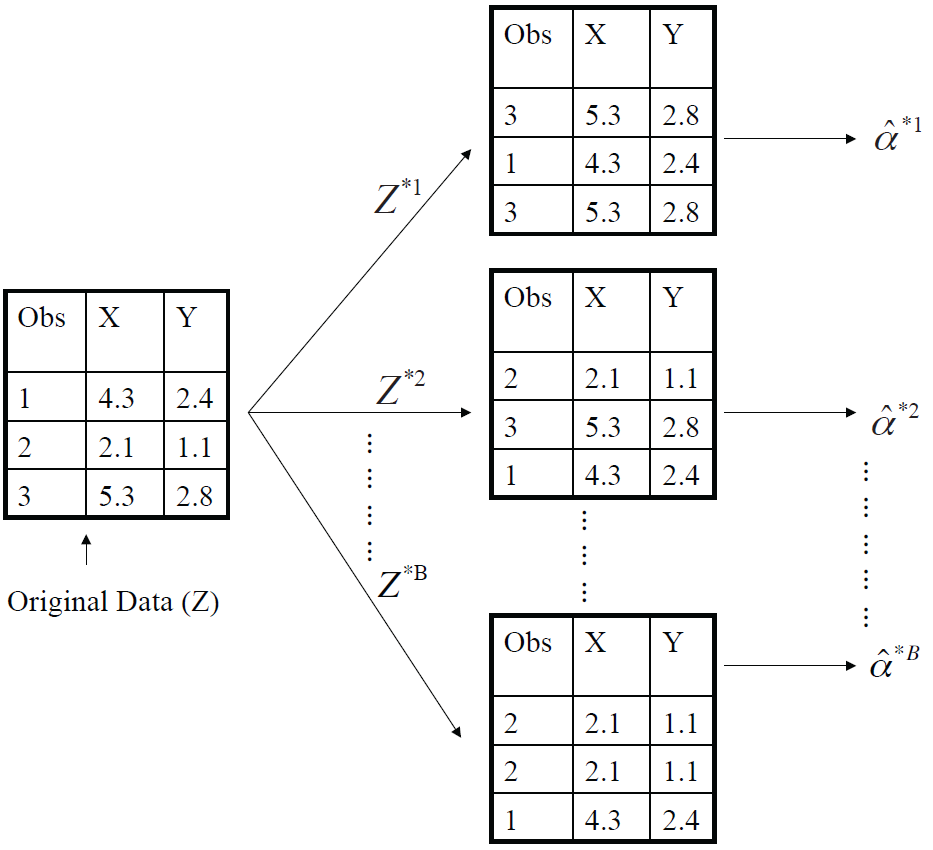
위 그림은 관측치가 달랑 3개뿐인 (n=3) 간단한 Z data-set(Original Data)에 bootstrap 기법을 적용한 예이다.
bootstrap data-set ()을 만들기 위해, data-set Z 로부터 임의로 n개의 관측치를 선택한다.
: sampling방법은 original data-set으로부터 복원추출 (with replacement).
이 예에서, bootstrap data-set을 보면, 3번째 관측치가 두번, 첫번째 관측치가 한번, 두번째 관측치는 없다.
bootstrap data-set을 사용하여,
에 대한 새로운bootstrap 추정치(
)를 구한다.
어떤 큰 수 B를 정하고, 이 과정을 B번마큼 만큼 반복적으로 수행한다고 하면,
서로 다른 bootstrap data-set들을 사용하여 대응되는 bootstrap 추정치
구한다.
아래 공식을 이용하여 위의 bootstrap 추청치들의 표준오차(standard error)를 계산하면,
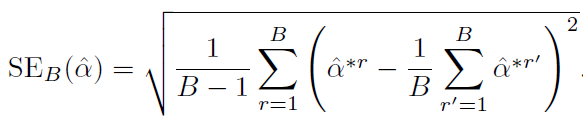
====================================
예제> 가장 좋은 투자배분 방식을 결정하는 예제
– X, Y(임의의 수)만큼의 수익을 내는 2개의 금융자산에 고정된 금액을 분산투자하고자 한다.
– 고정된 자금의 b 비율 만큼을 X 에, 나머지 1−b 만큼 Y에 투자한다.
두 자산에 대한 투자수익과 관련된 변동성이 존재하므로, 투자에 대한 전체 위험(또는 분산)을 최소화하는 b 를 찾고자 한다.
즉, 수식으로 표현하면 Var(bX -(1-b)Y) 를 최소로 만들려고 한다. 위험을 최소로 만들기 위한 식은 다음과 같고,
현실에서 구할수 없는 편차를 추정치로 대입하면,
여기서, 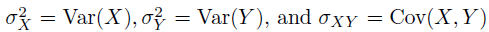
,
,
는 알수 없는 값이기 때문에, X와 Y의 과거 데이터를 값을 사용하여 X와 Y를 추정한다.
추정값을 위 식에 대입하고, 투자의 분산을 최소화하는 b 값을 추정하는 것이 목적이다.
simulated 데이터셋에서 α 를 추정하기 위한 기법을 설명
각 패널에는 X와 Y 100쌍 데이터에 대한 모의투자수익으로 표기했고, 이런 모의투자의 데이터를 이용하여 ,
,
를 추정하였다.
추정된 ,
,
을 위 식에 대입하여 b 추정치를 얻을 수 있다. 각각의 데이터로부터 얻어진
는 0.532에서 0.657의 범위를 갖는다.
b에 대한 추정치 는 시계방향으로 0.576, 0.532, 0.657, 0.651이다.
그럼 에 대한 얼마나 정확할까?
수량화된 정확성의 기준인 의 표준편차를 추정하기 위해,
100개의 쌍으로 구성된 X , Y 관측치를 생성하여 위 식에 대입하여 을 개산하는 과정을 1000번 반복한다.
이렇게 구한 1,000개의 (
)으로 히스토그램을 그려보면 아래 왼쪽그림과 같다.
이 모의실험을 위해 모수들을 =1,
=1.25,
=0.5로 설정되고,
=
= 0.6 True b 값은 0.6 이다라고 알수 있다.
True b는 히스토그램에서 실선으로 표기하고,
b에 대한 1,000개의 추정치( )의 전체평균은
=0.5996으로 True b값 0.6에 매우 가깝다.
추정치의 표준오차는 = 0.083 이 결과SE(
)는
의 정확도라고 할수 있다.
5.3.4 The Bootstrap
library(ISLR)
### DATA Loading
data("Portfolio")
str(Portfolio); head(Portfolio)
'data.frame': 100 obs. of 2 variables:
$ X: num -0.895 -1.562 -0.417 1.044 -0.316 ...
$ Y: num -0.235 -0.885 0.272 -0.734 0.842 ...
X Y
1 -0.8952509 -0.2349235
2 -1.5624543 -0.8851760
3 -0.4170899 0.2718880
4 1.0443557 -0.7341975
5 -0.3155684 0.8419834
6 -1.7371238 -2.0371910
통계량(Statistic)의 정확성 추정
bootstrap 접근법의 가장 큰 강점은 복잡한 수학계산없이도 거의 모든 경우에 적용이 가능하다라는 것이다
R에서 bootstrap 분석을 실행하려면 두단계 작업이 필요하다.
1. 통계량을 계산하는 함수 생성
2. boot()을 사용하여, 관측값들을 반복적으로 복원추출하는 bootstrap 수행
1. 통계량을 계산하는 함수 생성 – b.fn()
b.fn() 함수는 input으로 data와 index를 받고, ouput으로 b의 추정값 return 한다.
– input data: (X, Y)데이터
– input index: 어떤 관측값이 b를 추정하기 위해 사용되어지를 보여주는 벡터
– output : 선택된 관측값에 기반하여 α의 추정값을 return
b.fn <- function(data,index){
X <- data$X[index]
Y <- data$Y[index]
return ( (var(Y) - cov(X,Y)) / (var(X)+var(Y)-2*cov(X,Y)) ) # estimate b
}
b.fn(Portfolio, 1:100) 은 100개의 관측값 모두를 사용하여 b 추정한다.
b.fn(Portfolio, 1:100)
[1] 0.5758321
seed를 정하고, sample()을 사용하여 1~100까지 관측값을 임의로 복원추출한다.
=> 이는 새로운 bootstrap 데이터셋을 만들어 b 추정값을 다시 계산하는 것과 같다.
library(boot) set.seed(1) b.fn(Portfolio, sample(x=100,size=100,replace=TRUE,prob=NULL))
[1] 0.5963833
2. boot()을 사용하여, 관측값들을 반복적으로 복원추출하는 bootstrap 수행
boot()는 위와 같은 작업을 여러번 실행하여 b 에 대응하는 모든 추정값을 구하고, 표준편차를 계산하게 해 준다.
b에 대한 R=1000인 bootstrap 추정치
output 을 보면 원래 데이터를 사용하면, = 0.575821이고,
SE() 의 bootstrap 추정치는 0.08861826
boot(data=Portfolio, statistic=b.fn, R=1000)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = Portfolio, statistic = b.fn, R = 1000)
Bootstrap Statistics :
original bias std. error
t1* 0.5758321 -7.315422e-05 0.08861826
대략적으로 말하면, 모집단으로부터 하나의 random sample 에 대하여 은 b 와 평균적으로 약 0.08 만큼 차이가 난다고 기대할 수 있다.
그러나 현실에서는 위에서 구한 SE()을 estimating 절차는 적용불가하다.
왜냐면, 실제데이터에서는 원래의 모집단으로부터 새로운 데이터를 생성할 수 없기 때문이다.
그러나 bootstrap approach는 컴퓨터를 사용하여 새로운 sample set들을 얻는 방법을 모방하여 실행(에뮬레이트)하기 때문에
추가적인 표본을 생성하는 것 없이도 의 변동을 추정할수 있다.
bootstrap 추정치 SE()는 0.088이고, 1,000개의 모의 데이터셋을 이용하여 얻은 추정치 0.083과 매우 비슷하다.
<ALL>
#05.03.R
library(ISLR)
### DATA Loading
data("Portfolio")
str(Portfolio); head(Portfolio)
#############################################################################
b.fn <- function(data,index){
X <- data$X[index]
Y <- data$Y[index]
return ( (var(Y) - cov(X,Y)) / (var(X)+var(Y)-2*cov(X,Y)) ) # estimate b
}
b.fn(Portfolio, 1:100)
#install.packages("boot")
library(boot)
set.seed(1)
b.fn(Portfolio, sample(x=100,size=100,replace=TRUE,prob=NULL))
boot(Portfolio, b.fn, R=1000)
===================================================================
boot.result<-boot(data=Portfolio, statistic=b.fn, R=1000)
head(boot.result$t)
ggplot(data = NULL, aes(x=boot.result$t))+ ggtitle("estimates of b") +
geom_histogram( binwidth=0.04, fill="steel blue", color="black") +
geom_vline(xintercept=boot.result$t0, colour="pink", linetype="longdash") +
geom_vline(xintercept=0.60, colour="red") +
xlab("b")
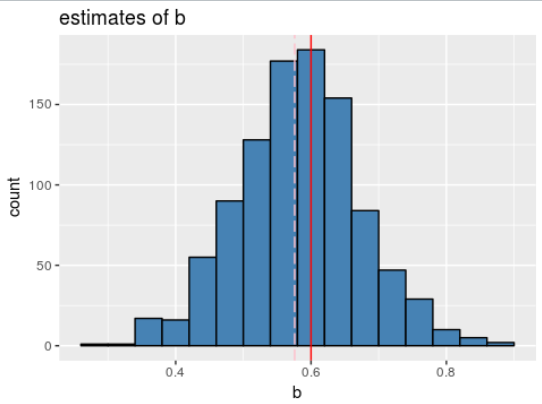
bootstrap 접근법이 와 관련된 변동성을 효과적으로 추정하는데 사용될 수 있음을 말해준다.