FFT (Fast Fourier transform)

https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/fft
https://youtu.be/VYpAodcdFfA – Two Effective Algorithms for Time Series Forecasting (Danny Yuan)
고속푸리에변환 [fast Fourier transform, 高速─變換] (두산백과)
https://m.blog.naver.com/umchinsu/221227664234

https://youtu.be/1JnayXHhjlg

• Fast (Discrete) Fourier Transform: 고속푸리에변환
• Computes the DFT(Discrete Fourier Transform, 이산푸리에변환) of an array with a fast algorithm
• 함수의 근사값을 계산하는 알고리즘.
  Fourier transform에 근거하여 근사공식을 이용한 DFT를 계산할 때, 연산횟수를 줄일 수 있도록 고안되었다
• 1960년대 중반 J.W.콜리와 J.W.터키에 의해 알려짐
• 여러 주기의 신호가 뒤섞여 있을 때 어떤 주파수 성분이 포함되어 있는지 알기 위해서 시간 영역의 신호를 주파수 영역의 신호로 변환하는 것
• 간단한 계산으로 영상 또는 아날로그 신호 등의 Fourier transform을 계산하기 위한 알고리즘
• 이산 푸리에 변환(discrete Fourier transform)을 효과적으로 얻어내는 수치적 방법
  

• Fourier transform : time함수 –> frequency함수(Amplitude, frequency, phrase)로 변환
• Inverse Fourier transform : frequency함수 –> time함수 로 변환
• 1초에 1번 진동 1Hz , 진동주기 1초,
• 1초에 10번 진동 10Hz, 진동주기 1/10초

LTI (linear time-invariant)

변환이란? 같은 현상을 다른방법으로 설명할수 있는 매핑. ex) 우리집 : 주소 , GSP위/경도.
Time Domain에서 어떤 연속적인 signal 은 frequency Domain의 여러 Sinusoids(정현파, 사인함수와 코사인 함수)의 합으로 변환이 가능하다.

Convolution, FFT

https://stackoverflow.com/questions/60198758/why-doesnt-this-r-code-produce-the-same-result-convolution-vs-fft
https://en.wikipedia.org/wiki/Convolution_theorem

x <- runif(10, 0, 1)
y <- runif(10, 0, 1)

Convolution = convolve(x,y, conj=F)

f <- fft( fft(x) * fft(y), inverse=TRUE)
FFT = Re(f)/length(f)                         ##not the same as convolve(x,y)....

all.equal(Convolution, FFT)  # TRUE

고속푸리에변환

h^m(0≤m≤N－1)이 복소수들의 집합일 때, 수열 {h^m}의 이산푸리에변환은 다음과 같다..

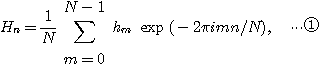
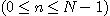
연속푸리에변환에서와 마찬가지 방법으로 이산변환도 다음과 같이 역변환을 구할 수 있다.

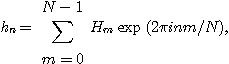
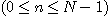
hⁿ은 역푸리에변환계수라 불린다. 고속푸리에변환의 알고리즘은 ①의 계산을 할 때 직적분해(direct product decomposition)를 이용하여 단계를 나누어 수행할 수 있다는 사실에 근거한다. N＝N₁N₂, N₁과 N₂가 서로 소일 때, 2차원의 푸리에변환계수를 예로 들어보자.

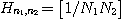
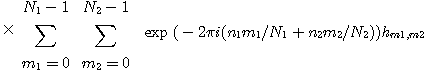
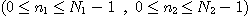
한 번의 복소곱셈과 복소덧셈을 하나의 기본연산으로 한다면, 호너의 방법(Horner’s method)을 사용했을 때는 N², 즉 (N₁N₂)²의 연산이 필요하나, 직적분해방법을 사용하면 N₁N₂(N₁＋N₂)의 연산으로H_n1,n2를 계산할 수 있다. 위 변환에 대응하는 행렬은 N₁×N₁과 N₂×N₂행렬의 직적(direct product)이므로, 다음 두 단계로 나누어 계산을 수행한다. 첫 단계로, 0≤m₁≤N₁－1과 0≤n₂≤N₂－1에 대하여

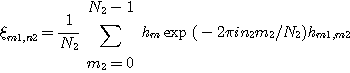
를 계산하고, 다음에 0≤n₁≤N₁－1과 0≤n₂≤N₂－1에 대하여

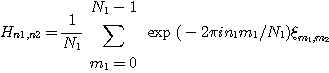
를 계산한다.