Dijkstra 다익스트라

Dijkstra’s algorithm

Intro

Dijkstra알고리즘은 그래프에서 최단 경로를 찾는 알고리즘으로,
이 알고리즘은 네트워크, 전송, 라우팅 등 다양한 분야에서 사용되며, 그래프 내에서 노드 간 최단 경로를 효율적으로 찾을 수 있습니다.

다익스트라 알고리즘의 개발 배경은 1956년에 네덜란드의 암스테르담에 위치한 Mathematisch Centrum (수학 센터)에서의 프로젝트였습니다. 당시 프로젝트는 도시 간의 최단 경로 문제를 해결하기 위한 방법을 찾는 것이었습니다. Edsger W. Dijkstra는 이 프로젝트를 위해 다익스트라 알고리즘을 개발하였습니다.

Dijkstra가 1959년에 처음으로 발표한 논문인 “A Note on Two Problems in Connexion with Graphs”에서 자세히 설명되었습니다. 이 논문은 최단 경로 알고리즘에 대한 체계적인 접근 방법과 개념을 제시하였습니다. 이후 컴퓨터 과학 분야에서 널리 사용되며, 최단 경로 문제의 핵심적인 알고리즘으로 자리매김하였습니다.

다익스트라 알고리즘은 우선순위 큐를 사용하여 효율적으로 구현할 수 있으며,
그래프의 모든 노드를 방문하지 않고도 최단 경로를 찾을 수 있는 특징이 있습니다.

다익스트라 알고리즘의 개발은 그래프 이론과 최적화 분야에 큰 영향을 미쳤으며, 더 나아가 네트워크와 전송 분야에서도 중요한 역할을 수행하고 있습니다

작동방식

1. Line(Edge)로 연결된 서로 다른 Node(point)가 있는 그래프가 있다고 가정할때,
   각 Line에 연관된 Weight 또는 Cost가 있습니다.
2. 시작하는 특정노드인 “source”Node 에서 “destination” Node까지의 최단 경로를 찾으려고 합니다.
3. (거리가 0인 소스 노드 자체를 제외하고) source node에서 다른 모든 node까지의 거리를 무한대로 설정합니다.
4. 이제 소스 노드의 이웃을 검사하고 거리를 업데이트합니다.
   소스 노드에서 현재 노드까지의 거리와 그 사이의 가장자리 가중치의 합으로 거리를 설정합니다.
5. 다음으로 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택하고 이웃에 대해 4단계를 반복합니다.
   이 과정을 계속하면서 점차적으로 노드 거리를 방문하고 업데이트합니다.
6. 대상 노드에 도달하거나 그래프의 모든 노드를 방문할 때까지 각 노드에서 찾은 최단 거리를 추적합니다.
7. 모든 노드를 방문하거나 목적지 노드에 도달하면 소스 노드에서 목적지 노드까지의 최단 경로를 찾은 것입니다.

간단히 말해서 Dijkstra 알고리즘은 소스 노드에서 시작하여 그래프를 탐색하고 점진적으로 거리를 업데이트하여 각 노드까지의 최단 경로를 찾습니다. 그것은 항상 각 단계에서 가능한 최단 경로를 선택하여 도로망에서 길을 찾는 것과 같습니다.

예제

import heapq

def dijkstra(graph, start_node):
    # start_node부터 최단거리를 저장하기 위해 "distance" 딕션너리 생성
    # {'A': 0, 'B': inf, 'C': inf, 'D': inf, 'E': inf}
    distances = {nodeNm: float('inf') for nodeNm in graph}
    distances[start_node] = 0

    # Create a priority queue to store the nodes to visit
    # [(0, 'A')]
    queue = [(0, start_node)]
    while queue:
        # using heap 자료구조 (우선순위 queue)
        current_distance, current_node = heapq.heappop(queue)
        # Skip if the distance to the current node is already smaller
        if current_distance > distances[current_node]:
            continue
        # Explore neighbor_nodes and update distances
        for neighbor_node, weight in graph[current_node].items():
            # neighbor_node = 'B';  weight = 5
            distance = current_distance + weight

            # Update distance if a shorter path is found
            if distance < distances[neighbor_node]:
                distances[neighbor_node] = distance
                heapq.heappush(queue, (distance, neighbor_node))
    return distances

graph = {
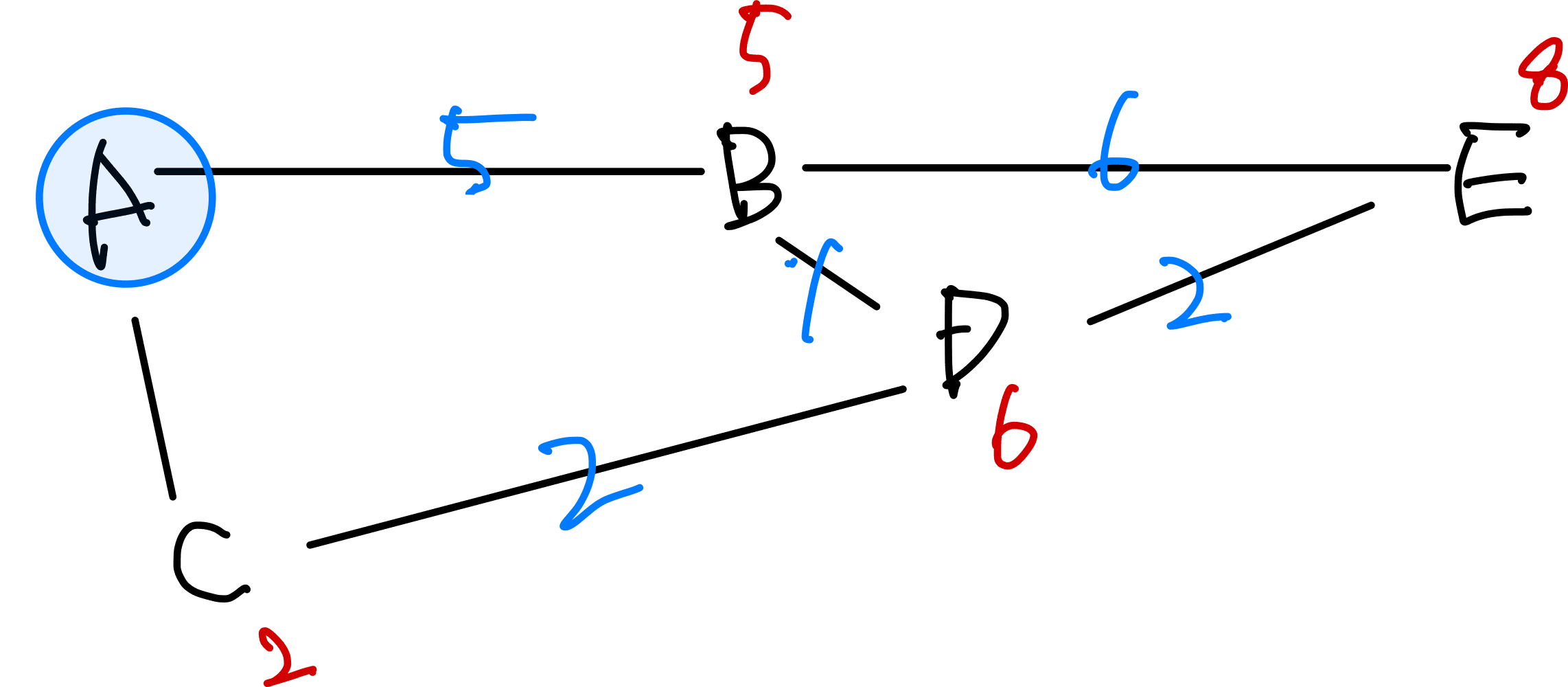
    'A': {'B':5, 'C':2},
    'B': {'A':5, 'D':1, 'E':6},
    'C': {'A':2, 'D':6},
    'D': {'B':1, 'C':6, 'E':2},
    'E': {'B':6, 'D':2}
}

start_node = 'A'
shortest_distances = dijkstra(graph, start_node)

print(shortest_distances)
# {'A': 0, 'B': 5, 'C': 2, 'D': 6, 'E': 8}