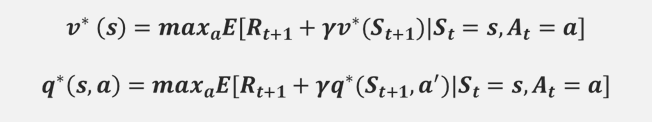Bellman (벨만 기대) 방정식
MRP
MDP – 상태가치함수 :V?(s), Q함수 : Q?(s,a)
https://dana-study-log.tistory.com/category/강화학습
가치함수를 계산해 낼수 있다면, 쉽게 더 가치가 높은 (Return이 큰) State를 고를 수 있다.
(상태)가치함수식에서 유도
[현재 state의 (상태)가치함수]와 [다음 state의 (상태)가치함수] 간의 관계를 식으로 나타낸 것 : recurrence relation(점화식)V?(s) = ??~?[Gt | St =s] trajectory ? 는 괘적의 확률과정이 정책 policy ?에 의존한다는 의미
Gt = Rt+1 + ?∙Rt+2 + ?2∙Rt+3 + ?3∙Rt+4 + … + ?T-1∙Rt+T
Gt = Rt+1 + ?∙Rt+2 + ?2∙Rt+3 + ?3∙Rt+4 + … + ?T-t-1∙RT

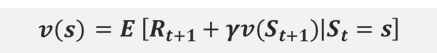
추가적으로, 특정 State에서 어떤 Action을 하는지에 따라 Reward이 달라지므로, 가치함수는 항상 정책에 의존한다.
따라서 “정책”까지 아래첨자로 수식에 표기한, 아래 수식이 벨만 기대 방정식이다.
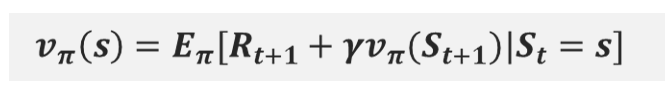
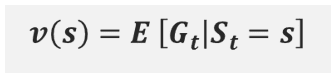
위의 수식을 살펴보면 [다음 상태의 기대함수]를 통해 [현재 상태의 기대함수]를 도출한다.
따라서, 벨만 기대 방정식은 [현재 상태의 가치함수]와 [다음 상태의 가치함수]간의 관계를 식으로 나타낸 것
왜 벨만 기대 방정식은 굳이 “가치함수를 변형”해 만들었는지?
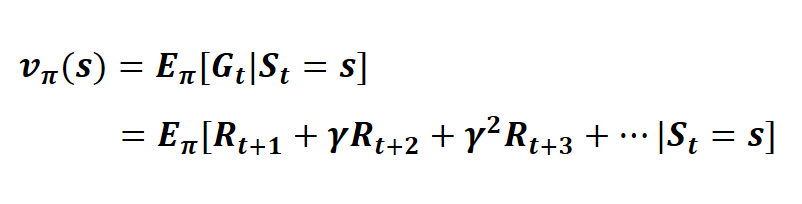
위 가치함수의 정의로부터 기댓값을 계산하려면, 앞으로 받을 모든 보상에 대해 고려해야 하는데,
이는 상태가 많은 환경에서는 상당히 비효율적인 방법이다.
따라서 하나의 수식으로 풀어내는 이 방법보단,
벨만 기대 방정식의 수식을 활용하여 여러 번의 연속적인 계산으로 가치함수의 참 값을 알아내는 방법이 효율적이다.
벨만 방정식은 [다음 상태의 가치함수]를 통해 [현재 상태의 가치함수]를 계산하는 구조를 가지고 있기 때문에
이미 저장되어있는 [다음 상태의 가치함수]를 이용해서 [현재 상태의 가치함수]를 계산한다.
처음에는 정확한 가치함수값을 얻지 못하지만, 이 과정을 여러번 진행하다보면 참 가치함수의 값에 수렴하게 된다.
즉, 벨만 기대 방정식에서 ‘=’ 등호 표시는 코딩에서의 = 인 ‘대입’의 개념이다.
다시 말해 [현재 상태의 가치함수]가 참 가치함수가 될 때까지, [다음 상태의 가치함수]를 이용한 수식(우항)을
[현재 상태의 가치함수]에 대입하여 업데이트시킨다는 뜻이다.
*여기서 “참 가치함수”란?
특정 상태의 가치에 대한 예측 정확도가 높은 가치함수
벨만 기대 방정식 의 다른 표현
MRP에서의 value function..을 활용
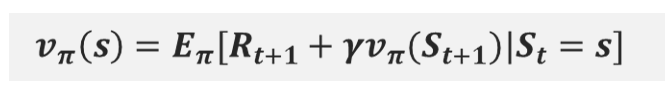
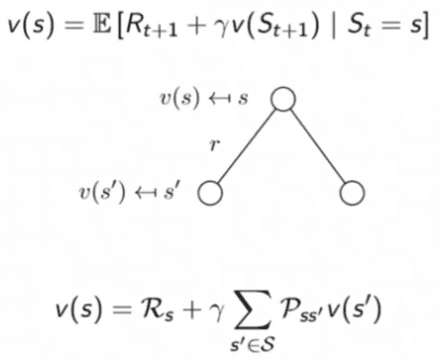
MDP에서의. policy를 고려한 가치함수
위 식처럼 “기댓값”으로 표현되어 있는 벨만 기대 방정식을 코딩이 가능하도록 다르게 표현해 보면,
기대값 = ∑ [( 각 사건이 벌어졌을 때의 이득) * (그 사건이 벌어질 확률) / 전체 사건]
= ∑ [ (현재 상태의 반환값인 Gt) * (어떤 행동을 할 확률인 정책 π(a|s)) ]


이때 Gt (현재 상태의 반환값)에 다음 상태의 가치함수가 포함되어있고, 여기에도 기댓값을 내포하고 있으니 같은 과정을 적용하는데,
여기서는 사건이 벌어졌을 때의 이득에 해당하는 부분은 (반환값이 아니라) 저장되어있는 다음 상태에 대한 가치함수를 이용하고,
사건이 벌어질 확률은 상태 변환 확률을 이용한다.
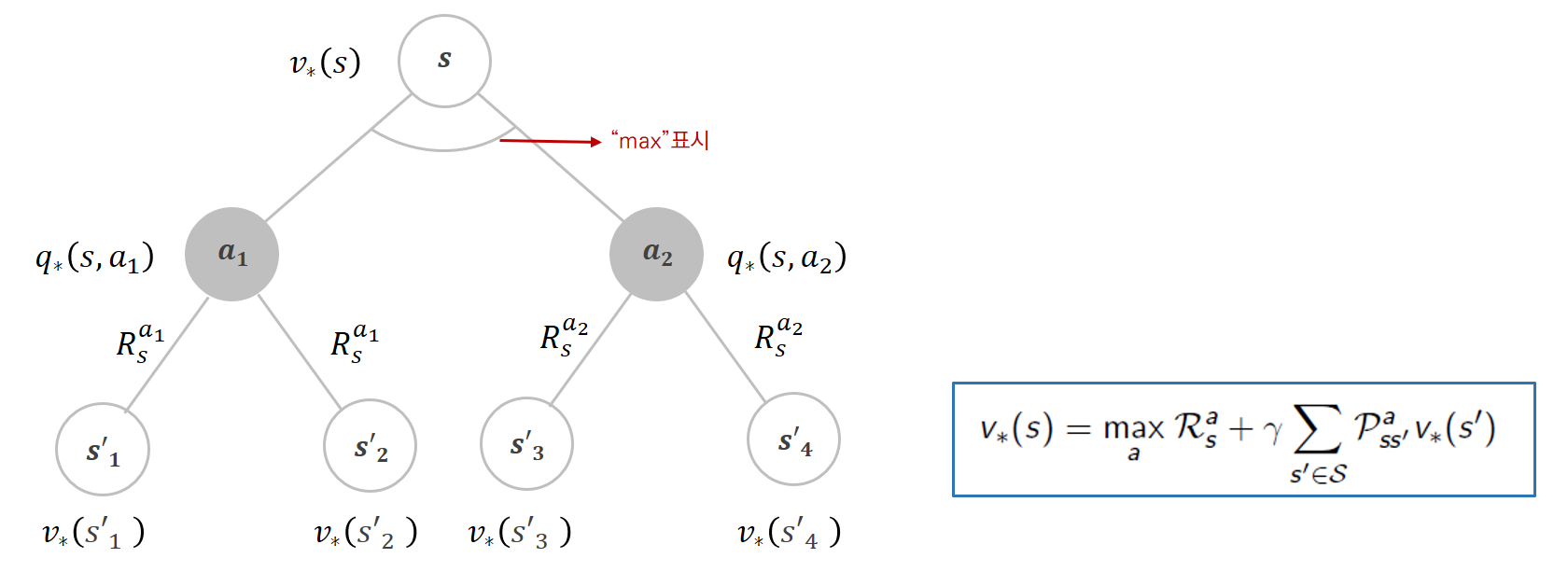
위의 내용을 좀 더 쉽게 그림을 통해 알아보자.
흰 노드 : 상태 s
회색 노드: 상태 s에서 선택한 Action
상태 s에서 뻗어나가는 가지: 각각의 행동의 개수만큼이다.
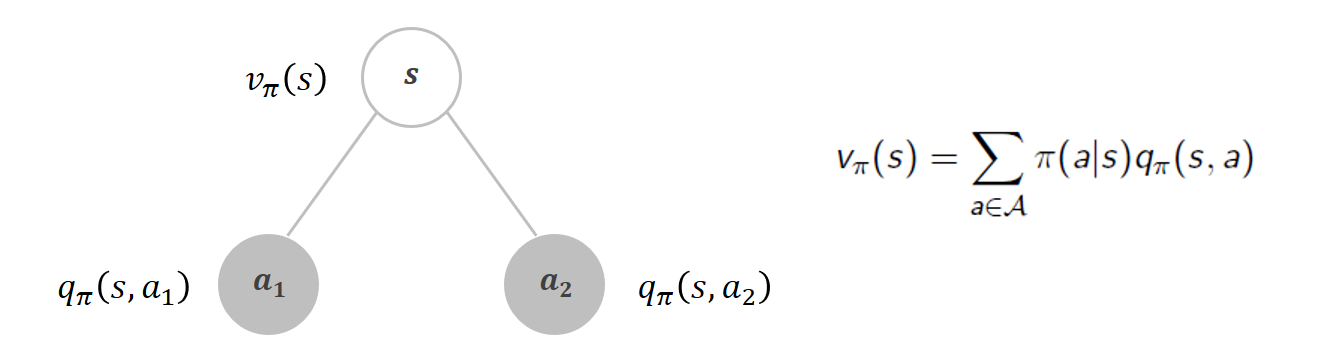
이때 (상태) 가치함수와 Q함수(행동 가치함수)의 관계는 오른쪽 식처럼 표현 가능하다.
각 행동을 할 확률 π(a|s)와 그 행동을 해서 받는 Q함수값(예상되는 반환값)을 곱한 것을 모두 더하면,
현재 상태 s의 가치함수가 된다는 것이다.
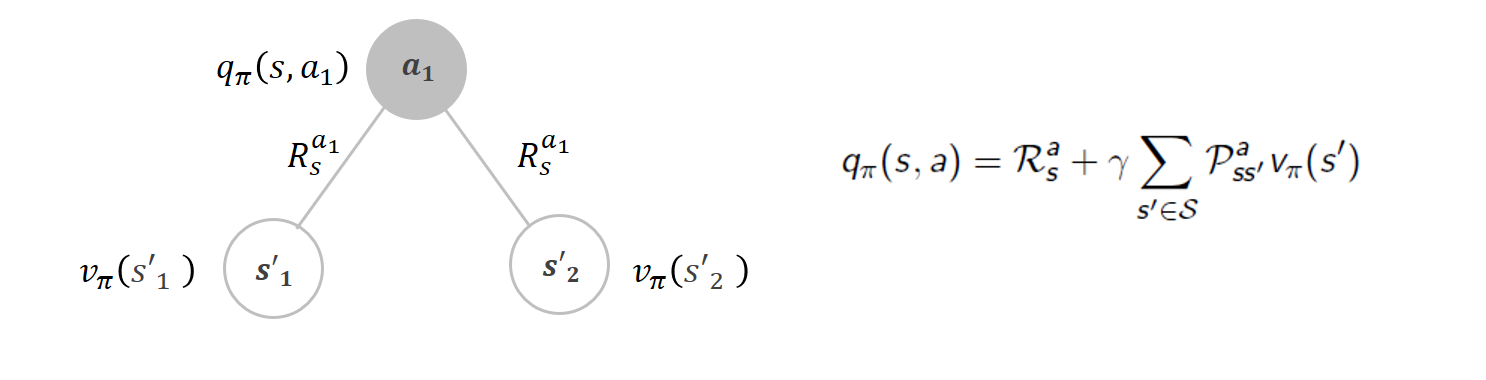
그런 다음, 각 행동을 선택한 후에는 Reward이 주어지는데, Reward을 출력하는 보상함수에는 상태와 행동이 조건으로 들어가기 때문에 행동 노드 아래에 표기되어있다.
행동에서 뻗어나가는 가지가 여러개인 것은 외부적인 요인에 의해 다른 상태로 갈 수 있기 때문이다.
=> “상태 변환 확률”이 1이어서 행동한 대로 무조건 정해진 다음 상태가 나타나는 deterministic한 환경이 아니라!
따라서 Q함수는 오른쪽 수식과 같이 특정 행동을 한 뒤 즉시 받는 보상에 행동을 통해 각 다음 상태로 갈 확률 곱하기 해당 다음 상태의 가치함수를 더한 것(한 스텝 지나서 감가율 적용)으로 표현할 수 있다.
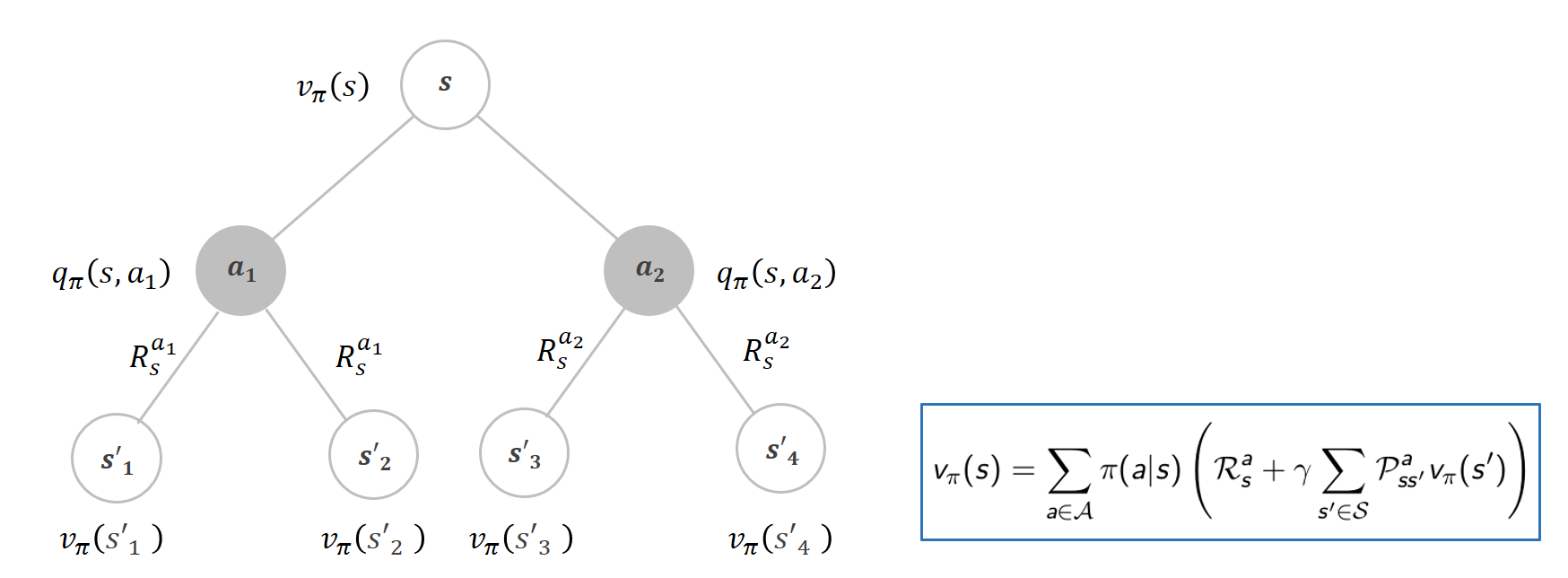
위 두 개념을 합치면, “현재상태의 가치함수”는 “다음 상태의 가치함수”와 상태 변환 확률, 정책을 모두 고려하여 계산할 수 있다.
지금까지 벨만 기대 방정식은 보상과 상태 변환 확률을 모두 미리 알고 있어야 한다.
이러한 정보들을 MDP의 model이라고 하는데 모델을 미리 알고 있는 model-based 한 환경에서만 벨만 방정식을 구할 수 있다.
Q함수(행동 가치함수)도 벨만 방정식의 형태로 표현
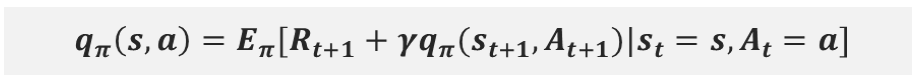

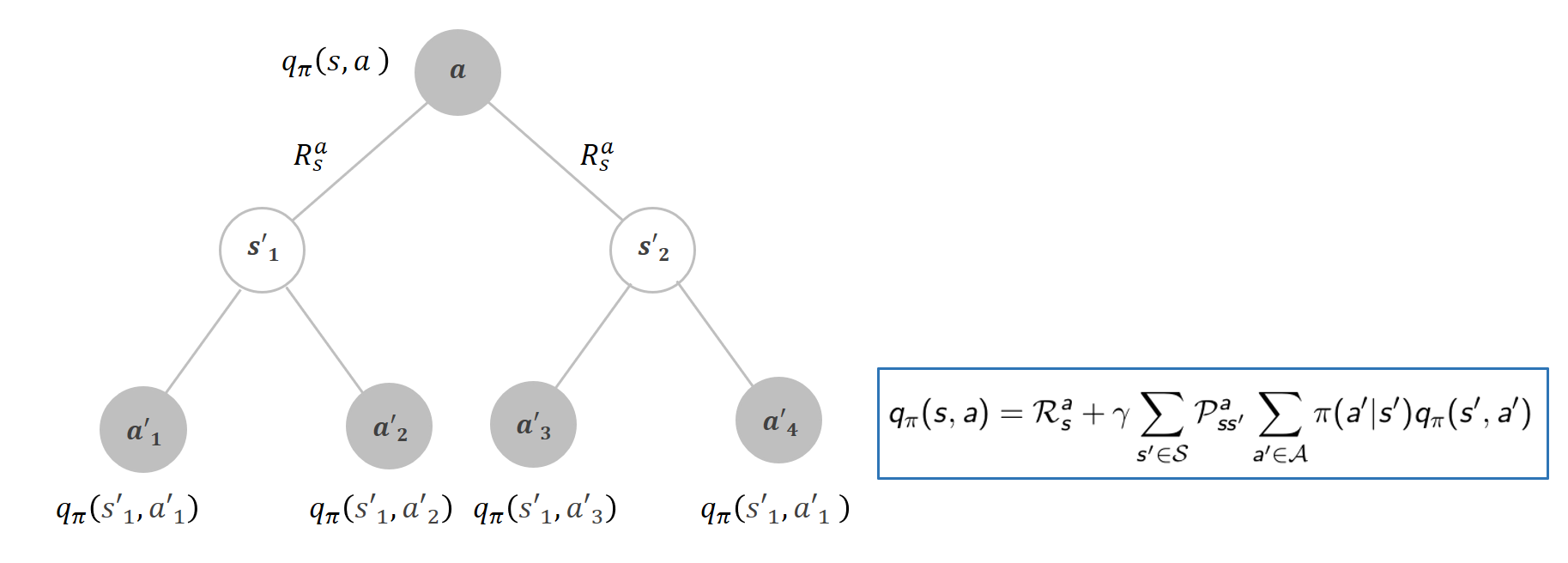
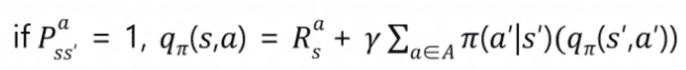
같은 내용을 Q함수에 대해서 표현한 그림이다.
벨만 기대 방적식 (계산)
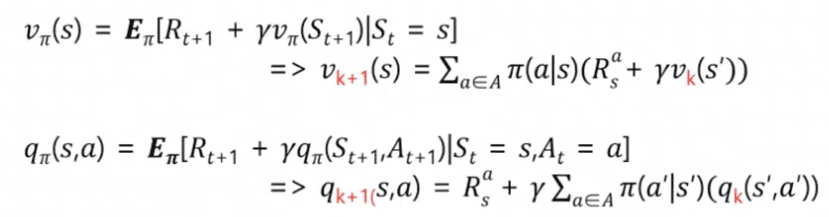
정책 ? 를 따를때의 상태가치함수 –(수렴)–> 참 가치함수
Agent가 가장 높은 보상을 주는 ?*(최적의 정책) 을 알고자 하는 것이기 때문에, max?[??(s)] 가 바로 ?*(s)이다.
벨만 최적 방정식
최적 가치함수 vs. 최적 Q함수
벨만 최적 방정식을 이야기하기 전에, 최적 가치함수에 대해 먼저 알아보자.
강화학습의 목적은 앞으로 받을 보상들을 최대로 하는 정책을 찾는 것이다.
“최적 가치함수“란 현재 상태에서 앞으로 가장 많은 보상을 받을 정책을 따랐을 때의 가치함수이다.
즉, 현재 환경에서 취할 수 있는 가장 높은 값의 보상 총합이다.
“최적 Q함수”도 마찬가지로 현재 (s,a)에서 얻을 수 있는 최대의 Q함수이다.
Agent는 각 상태 s에서 최적Q함수 중 가장 큰 Q함수를 가진 행동을 하는 것이 최적 정책이 된다.
선택 상황에서 판단 기준은 Q함수가 되는 것이다.
최적 가치함수 vs. 참 가치함수
최적 가치함수와 위에서 언급했던 참 가치함수를 정리하면 아래와 같다.

벨만 최적 방정식
벨만 최적 방정식은 (벨만 기대 방정식처럼) 최적 가치함수를 [현재 상태의 최적 가치함수]와 [다음 상태의 최적 가치함수] 사이의 관계로 나타낸 식이다.