PCA 의 기본
- PCA는 차원축소에 많이 사용되지만, (PCA가 차원을 실제로 차원을 축소해 준다기 보다는)
PCA의 결과에서 차원을 선별적으로 사용한다고 이해하는 것이 좋다. - PCA는 분산이 크기로 각 차원의 데이터에 대한 설명력을 보여준다.
- PCA는 서로 직교(독립)하는 Linear 축을 찾기위해 선형변환하는 것이다.
- 즉, 각 차원의 축(PC)은 변수들의 선형결합(linear combination)이고,
X가 서로 이미 상관관계가 높지 않다면(correlation, off-diagonal 값이 0에 가까운) PCA할 이유가 없다. - (계산상으로) 직교하는 각 차원의 축(PC)는 데이터의 eigenVector이고,
설명력은 대응되는 eigenValue이다.
DATA example
예제데이터는 학생 100명의 물리학 성적과 통계학 성적이다.
Obs의 갯수 n=100 (100명의 학생), 변수의 갯수p가 2 (ex, Phys성적, Stat성적)
URL <- "https://raw.githubusercontent.com/steviep42/youtube/master/YOUTUBE.DIR/marks.dat" dd <- fread(URL)
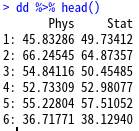
Phys Stat
1: 45.83286 49.73412
2: 66.24545 64.87357
3: 54.84116 50.45485
...
98: 29.57351 35.60014
99: 46.26462 41.10685
100: 53.31890 48.86226
Phys StatVisualization
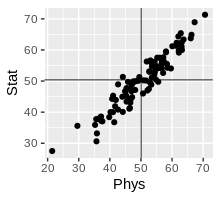
Original
meanPhys <- mean(dd$Phys)
meanStat <- mean(dd$Stat)
dd %>% ggplot(aes(Phys, Stat)) + geom_point() +
geom_hline(yintercept=meanPhys, size=.3) +
geom_vline(xintercept=meanStat, size=.3) +
coord_equal()
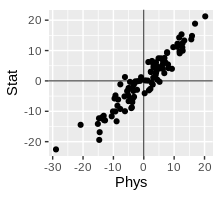
Centered (but, Not Scaled)
원래, PCA할 데이터는 표준화가 필요하다. 중심화(평균=0, center=T), 스케일 (표준편차=1, scale.=T)
이 예제에서는 일단 데이터를 중심화하고, 단위가 같기때문에 굳이 scale하진 않는다.(PCA default세팅과 같음)
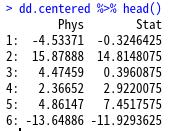
dd.centered <- dd[ ,lapply(.SD, function(x){(x-mean(x))})]
# 참고
#dd.standardize <- dd.centered.scaled <- dd[ ,lapply(.SD, function(x){(x-mean(x))/sd(x)})]
dd.centered %>% ggplot(aes(Phys, Stat)) + geom_point() +
geom_hline(yintercept=0, size=.3) +
geom_vline(xintercept=0, size=.3) +
coord_equal()","showLines":false,"wrapLines":false,"highlightStart":"6","highlightEnd":"7
PCA의 결과 활용
pr <- prcomp(dd) # center=T, scale.=F
#pr.centered <- prcomp(dd.centered) # all.equal but pr.centerd$center
data.table(pr$x) %>%
ggplot(aes(PC1, PC2)) + geom_point(color="blue") +
geom_point(data=dd.centered , aes(Phys, Stat), color="grey", alpha=0.6) +
coord_equal() + geom_hline(yintercept=0, size=.3) + geom_vline(xintercept=0, size=.3)
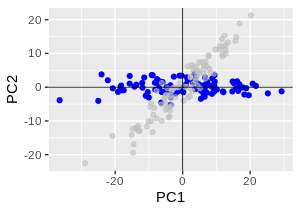
예제의 Original 데이터가 2차원이므로,
구할수 있는 PC1 PC2로 plotting하면,
선형변환을 통해 정확하게 회전만 된것으로 보여질 수 있다.
pr <- prcomp(dd, center=F) predict(pr)[1:6,] # = Score = pr$x as.matrix(dd[1:6, ]) %*% pr$rotation # = predict(pr)[1:6,] predict(pr)[1:6,] %*% solve(pr$rotation) # = dd[1:6, ] 원데이터로 원복
PCA 의미
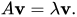
A : 어떤 행렬
v : eigenVector
lamda : eigenValue
A : 어떤 행렬
V : eigenVectors 로 이루어진 행렬
Λ : diag() :eigenValues로 만든 대각행렬
A : 데이터의 coVariance/corRelation M, 변수들의 내적
==> cov(dd)
R : 변수의 Loading M, Rotation M, 데이터의 선형변환 , coVariance의 eigenVector
==> pr$rotation
Λ: PC의 분산으로 만든 대각행렬, 각 축의 설명력
==> diag(pr$sdev^2)
symmetric_origin <- matrix(c(-1, 0, 0, -1), nrow=2, ncol=2, byrow=T)
symmetric_xAxis <- matrix(c( 1, 0, 0, -1), nrow=2, ncol=2, byrow=T)
symmetric_yAxis <- matrix(c(-1, 0, 0, 1), nrow=2, ncol=2, byrow=T)
symmetric_y_x <- matrix(c( 0, 1, 1, 0), nrow=2, ncol=2, byrow=T)
cov(dd) %*% pr$rotation
diag(pr$sdev^2)%*% pr$rotation # same as above
eigenV <- eigen(cov(dd))
diag(eigenV$values) %*% eigenV$vectors %*% symmetric_origin
* Pr$x (= Scores) (=PC1 PC2... Value of the rotated data , rotated variables)
centred(또는 scaled까지)된 Original data 에 rotation matrix를 곱해서 얻은 값 (retx=TRUE일때)
pr$x # the value of the rotated data
as.matrix(dd.centered) %*% pr$rotation # same as above,
# 중심화된 Data에 rotation 행렬을 곱한값, 선형변환된 결과
# 실제 Phys점수 * PC1의 Phys + 실제 Stat점수 * PC1의 Stat
predict(pr) # same as above, Predict값
#(the centred(& scaled)data multiplied by the rotation matrix)
따라서, 이미 회전을 통해 서로 Orthogonal한 축을 만들었기 때문에 cov(pr$x) 는 분산만 존재하는 diagonal matrix가 된다. 즉 diag(pr$sdev^2)
cov(pr$x) # cov( as.matrix(dd.centered) %*% pr$rotation )
diag(pr$sdev^2) # all.equal
각 PC의 설명력은 분산이고, %로 나타내면 다음과 같다.
pr$sdev^2 #설명력, dd의 eigen-value
(pr$sdev^2)/sum(pr$sdev^2)*100
변수<데이터 변수>데이터
pr$rotation 변수갯수* PC갯수(변수갯수) 변수갯수* PC갯수(데이터수)
pr$x 데이터수* PC갯수(변수갯수) , 데이터수* PC갯수(데이터수)
pr$sdev PC갯수(변수갯수) 데이터수
pr$center 변수갯수
pr$scale 변수갯수
| pccomp | princomp | acp | |
| rotation | loadings | loadings | the matrix of variable loadings (columns are eigenvectors) |
| eig | |||
| x | scores | scores | predict(pr) The coordinates of the individuals (obs.) on the principal components. |
| sdev | sdev | sdev | the standard deviations of the principal components |
| center | center | the variable means (means that were substracted) | |
| scale | scale | the variable standard deviations (the scaling applied to each variable ) |
참고> Data
(https://raw.githubusercontent.com/steviep42/youtube/master/YOUTUBE.DIR/BB_phys_stats_ex1.R)
그래픽으로 PCA 설명 : Explained Visually - http://setosa.io By Victor Powell with text by Lewis Lehe
txtString <- "
Phys Stat
45.83286 49.73412
66.24545 64.87357
54.84116 50.45485
52.73309 52.98077
55.22804 57.51052
36.71771 38.1294
70.60068 71.31107
46.58481 43.0755
37.61019 37.06575
54.4459 52.86622
42.65069 48.93422
54.37827 56.17238
55.48877 54.14389
54.75712 54.90254
58.49035 54.28524
36.50214 37.7616
57.46308 56.18982
50.88379 50.22294
66.00721 63.74446
40.21083 40.01258
62.80092 65.38431
52.6778 53.11069
46.37766 44.08331
62.1887 59.14436
67.25034 68.91049
46.94243 46.7534
40.7363 44.2691
44.16992 40.07929
63.06225 61.06836
21.46127 27.51049
53.06325 56.62534
46.75746 44.27409
42.62306 40.81727
37.1718 38.58767
35.69836 30.63126
45.89923 43.99144
58.04152 59.51573
54.64092 53.74517
41.41039 36.76394
63.12466 62.46416
41.00973 40.00774
44.99261 46.69961
44.93524 46.71632
37.29267 37.14477
58.34537 55.47421
53.43469 55.79567
45.36934 47.71729
52.06818 46.96069
49.16137 50.08758
51.86147 56.27546
56.58516 55.46879
41.69534 41.89212
62.34281 62.01932
39.80478 38.39744
56.0382 57.49428
44.01542 44.95353
45.22847 45.33766
61.32475 61.32643
45.68322 47.66341
48.14822 47.1341
57.17597 57.60514
46.44202 41.33925
35.24607 35.90807
55.56036 49.76122
41.04521 45.28572
51.67046 50.16363
52.93516 49.51824
35.84404 33.17955
47.15922 44.82814
60.08049 61.18417
55.10556 54.57818
50.66494 46.00166
63.17677 60.00211
49.47325 51.27673
44.17665 51.33226
35.61826 37.75184
47.6078 49.91266
62.02337 64.34087
47.17575 49.49582
59.63255 54.04946
46.66867 47.50897
41.92247 43.92537
58.06207 59.25163
63.70322 63.36367
53.54859 54.65436
54.28997 52.04134
61.45739 62.29298
48.42434 49.98111
47.02817 48.76383
56.68283 54.01947
47.39154 49.38044
53.48607 51.11642
57.12145 52.61662
62.14516 59.79395
52.54617 47.44484
56.72894 56.57045
45.37159 43.3991
29.57351 35.60014
46.26462 41.10685
53.3189 48.86226
"
dd <- read.table(file=textConnection(txtString), header=T) %>%data.table
closeAllConnections()library(tidyverse) library(data.table) # https://stats.stackexchange.com/questions/222/what-are-principal-component-scores txtString <- " Maths Science English Music 80 85 60 55 90 85 70 45 95 80 40 50 " dd <- read.table(file=textConnection(txtString), header=T) %>% as.data.table() closeAllConnections() dd pr <- prcomp(dd, scale. = T) pr$x pr$rotation pr$sdev cov(dd) %*% pr$rotation symmetric_origin <- matrix(c(-1, 0, 0, -1), nrow=2, ncol=2, byrow=T) symmetric_xAxis <- matrix(c( 1, 0, 0, -1), nrow=2, ncol=2, byrow=T) symmetric_yAxis <- matrix(c(-1, 0, 0, 1), nrow=2, ncol=2, byrow=T) symmetric_y_x <- matrix(c( 0, 1, 1, 0), nrow=2, ncol=2, byrow=T)