A Generic Cycle Life Model for Lithium-Ion Batteries Based on Fatigue Theory and Equivalent Cycle Counting
https://ieeexplore.ieee.org/document/9163253
ABSTRACT
이 논문은 리튬 이온 배터리의 수명 주기 모델을 제안합니다.
이 연구의 주요 목적은 리튬 이온 배터리의 노화(사이클링으로 인한)와 배터리 용량 및 내부 저항에 미치는 영향에 대한 전기적 시뮬레이션을 용이하게 하는 것입니다.
현재까지의 수명모델의 제약사항 :
보고된 대부분의 사이클 수명 모델은 매개변수 검색이 어려운 물리학 기반이거나, 매개변수 식별 프로세스에 많은 양의 실험 데이터와 막대한 인력, 수개월에서 수년에 걸친 테스트 기간이 필요한 반경험적 모델입니다. 또한 이러한 모델은 기본 배터리에만 유효하고 다른 배터리 유형에는 적용되지 않는 경향이 있습니다. 따라서 리튬 이온 배터리 사이클링 효과의 시뮬레이션은 달성하기 어렵고 비용과 시간이 많이 소요됩니다.
이 논문에서 제안하는 모델은 피로 이론과 등가 사이클 카운팅의 간단한 물리 방정식을 기반으로 합니다.
매개변수 식별 프로세스는 간단하며 배터리 데이터시트의 몇 가지 데이터와 제한된(또는 짧은 기간의) 사이클링 실험만 필요합니다.
제안된 모델은 일반적이며 방전 깊이(DoD), 온도 및 C-rate과 같은 일반적인 사이클 수명 요소의 영향을 나타낼 수 있습니다.
이 모델은 두 가지 리튬 이온 배터리 유형(LFP-LiFePO 4 및 NMC-LiNiMnCoO 2 )을 사용하여 검증되었으며 시뮬레이션 결과는 실험 결과와 비교하여 ±1.5% 이내의 오차로 실제와 가깝습니다.
리튬이온배터리의 cycle life model
- LFP-LiFePO4
- NMC-LiNiMnCoO2)
목적
- 배터리 aging의 전기(회로) 시뮬레이션 (물리적X, 경험적X)
- 배터리 용량과 내부저항에 대한 aging의 영향
제안하는 모델
- imple physical equations from fatigue theory
- equivalent cycle counting
- 포괄적인
- 일반적으로 영향을 주는 factor
- DoD (depth-of-discarge)
- temperature
- C-rate
Parameter 식별방법
- 간단,
- 배터리 datasheets의 소수 데이터
섹션 I. 소개
리튬 이온 배터리<Lithium-ion batteries>는
운송(자동차, 버스, 기차, 항공기 등), 휴대용 전자기기 및 백업 전력 시스템을 포함한 많은 애플리케이션에서 선택되는 에너지 저장 장치입니다. 이는 주로 에너지 및 전력 밀도가 높고 효율이 높을 뿐만 아니라 다른 배터리(NiCd, NiMH, Lead Acid납축전지)에 비해 자체 방전이 적기 때문입니다[1]-[6].
다른 배터리 유형과 마찬가지로, 리튬 이온 배터리의 에너지 및 전력 밀도는 노화에 따라 감소합니다.
이는 배터리가 노후화됨에 따라 배터리 용량과 내부 저항이 변화하기 때문입니다[7]-[12].
이러한 노화 효과는 배터리가 작동할 때 증폭되는데, 이는 주로 다양한 작동 조건에서의 사이클링으로 인해 발생합니다.
배터리가 작동하는 동안 배터리 충전 상태(SoC)를 올바르게 예측하고, 배터리의 생애동안의 부하 수요(the load demand)를 충족하기 위해서는 사이클 수명 모델이 필요합니다.
리튬 이온 배터리의 사이클 수명 모델은 여러 가지가 문헌에 보고되어 있습니다.
이러한 모델은 전기화학/물리 기반 또는 경험적/반경험적 기반입니다.
전기화학 또는 물리 기반 모델은 전극 부피, 분리막 두께, 이온 농도, 반응 속도 등 많은 심층 파라미터가 포함된 복잡한 미분 방정식을 사용합니다[13], [14]. 이러한 모델은 사이클링으로 인한 전극 및 전해질의 물리적 변화(예: 고체 전해질 간상(SEI) 층의 성장, 이온 및 활성 물질의 손실, 침전물 층의 성장, 전해질의 손실 등)와 배터리 셀 성능에 미치는 영향을 나타낼 수 있습니다.
그러나 이러한 모델은 모델 파라미터를 쉽게 구할 수 없고 검색하기 어렵기 때문에 전기 시뮬레이션에 현실적이지 않습니다.
경험적 또는 준경험적 모델은 대량의 실험 데이터와 준경험적 방정식 또는 룩업 테이블을 기반으로 합니다 [15]-[24]. [15]-[19]에서 제안된 Ah-처리량(또는 쿨롱 계수) 모델링 [Ah-throughput (or coulomb counting) modeling] 접근 방식이 이 범주에서 가장 많이 사용되는 예입니다.
이러한 모델에서 사이클링으로 인한 용량 손실과 저항 증가는 몇 가지 미지의 파라미터에 대한 경험적 방정식을 사용하여 추정됩니다. 파라미터를 식별하려면 일반적으로 통제된 테스트 환경에서 수년간의 사이클링 실험이 필요합니다. 따라서 이러한 모델을 특성화하는 데 많은 비용과 시간이 소요됩니다. 또한 [25] 및 [26]에서 입증된 바와 같이, 이러한 모델은 테스트 중인 특정 배터리에만 유효하고 다른 배터리 유형에는 적용되지 않는 경향이 있습니다.
일부 저자는 fatigue analysis[피로 분석]에 널리 사용되는 강우량 계수(RFC: rain flow counting) 알고리즘을 사용하여 배터리 사이클 수를 계산하는 사이클 수명 모델을 제안하기도 했습니다 [27], [28].
이러한 모델은 로딩 프로파일[ loading profile]에 대한 선험적 지식이 필요하기 때문에 오프라인에서만 사용할 수 있습니다. 따라서 배터리가 작동 중인 동안에는 사이클링이 배터리 용량과 내부 저항에 미치는 영향을 나타낼 수 없습니다.
이 논문에서는 피로 이론과 등가 사이클 카운팅[fatigue theory and equivalent cycle counting]의 물리 방정식에 기반한 사이클 수명 모델을 제안합니다.
모든 충전-방전 사이클에 대해 등가 사이클 수와 DoD, C-rate 및 온도와 관련된 스트레스 요인을 기반으로 노화 지수를 계산합니다.
그런 다음 이 노화 지수를 사용하여 배터리 용량과 내부 저항에 대한 사이클의 영향을 나타냅니다.
모델 파라미터는 배터리 데이터시트에 제공된 수명 주기(또는 용량 손실) 곡선과 제한된(또는 짧은 기간의) 사이클링 실험을 사용하여 도출됩니다. 이 모델은 일반적이며 모든 리튬 이온 배터리 유형에 사용할 수 있습니다.
Key contributions
이 백서의 주요 기여는 다음과 같습니다:
- 배터리 데이터시트[battery datasheet] 와 제한된(또는 짧은 기간의) 사이클링 실험을 사용하여 매개변수를 식별하기 위한 단순하고 빠른 접근 방식을 갖춘 사이클 수명 모델입니다. 대부분의 리튬 이온 배터리 데이터시트에는 수명 주기 곡선이 포함되어 있으므로 파라미터 식별 프로세스에 소요되는 시간이 줄어듭니다.
- 이 모델은 물리 방정식과 등가 사이클 카운팅을 기반으로 하므로 모든 유형의 리튬 이온 배터리에 적용할 수 있습니다.
- 이 연구는 [29]에서 보고된 이전 연구를 개선한 것으로,
배터리 모델 성능에 대한 사이클 효과를 나타내기 위해 사이클 수명 모델을 추가했습니다.
다음 섹션에서는 제안된 사이클 수명 모델에 대해 설명하고,
세 번째 섹션에서는 데이터시트 및 실험에서 모델 파라미터를 추출하는 절차를 보여주며,
마지막으로 네 번째 섹션에서는 실험 검증에 대해 설명합니다.
섹션 2: 사이클 수명 모델 : Cycle Life Model
그림 1은 제안된 사이클 수명 모델을 포함하는 [29]의 배터리 모델의 개선된 버전을 보여줍니다.
- Block A: 배터리 모델은 저항과 직렬로 연결된 가변 개방 회로 전압(E).
- 개방 회로 전압과 저항은 배터리 thermodynamics voltage 열역학 전압(E0), battery capacity배터리 용량(Q), internal resistance 내부 저항(R) 및 polarization constant편광 상수(K)에 따라 달라집니다.
E0, Q, R, K는 배터리 온도에 따라 달라지므로 이러한 파라미터를 추정하기 위해 [29]에 열 모델(BlockB-D)이 추가되었습니다.- Block C : 배터리에서 발생하는 열을 추정하고,
- Block B는 배터리 온도를 추정합니다.
- Block D는 추정된 배터리 온도를 사용하여 E0, Q, R, K를 계산합니다.
- 사이클 수명 모델(블록 E)은 배터리 수명에 따라 배터리 용량과 저항을 수정하는 데 사용됩니다.
이 백서에서는 사이클 수명 블록(블록 E)에만 초점을 맞춥니다.
다른 블록(A,B,C, D)에 대한 자세한 내용은 [29]에 나와 있습니다.
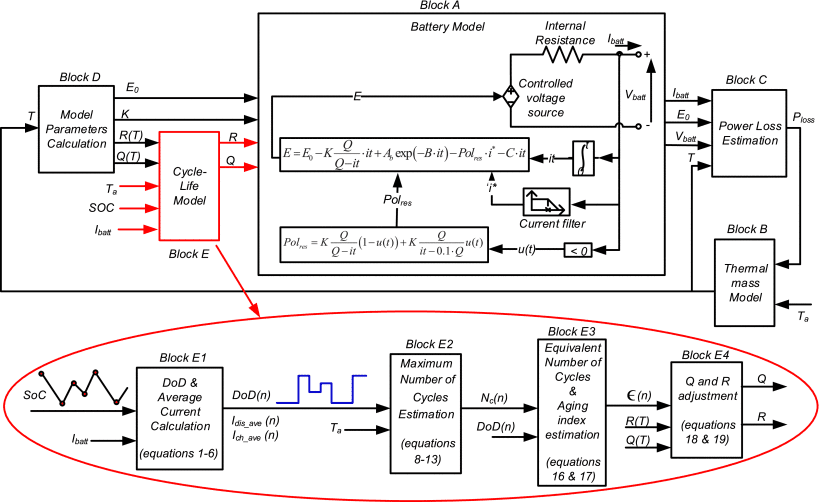
Figure 1. Proposed lithium-ion battery cycle life model.
사이클 수명 모델은 4개의 주요 블록(블록 E1, E2, E3-E4)으로 구성됩니다.
- 블록 E1은 각 사이클 동안 방전 깊이(DoD)와 평균 C-rate을 결정합니다.
- 블록 E2는 (주변 온도, DoD 및 C-rate과 관련된) 스트레스 요인을 기반으로 최대 사이클 수를 추정합니다.
- 블록 E4에서는 노화 지수에 따라 배터리 용량과 저항을 조정합니다.
- 블록 E3에서 등가 사이클 수 개념을 기반으로 노화 지수 (aging index)는 계산됩니다.
다음 섹션에서는 각 블록에 대한 모델링 방정식을 설명합니다.
A. (블록 E1) : DoD 및 평균C-rate 계산
DoD (%)+SoC (%)=100%
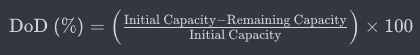
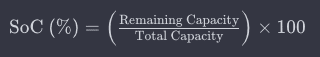
DoD(방전심도)는 maximum capacity(최대용량) 대비 배터리가 방전되는 정도를 측정한 것.
- Initial Capacity(초기 용량) : 배터리가 fully charged되었을 때, 원래 용량 original capacity
- Total Capacity(총 용량) : 배터리가 완전히 충전되었을 때의 최대 용량 maximum capacity
- Remaining Capacity(남은 용량): 현재 배터리 용량
예) 초기 용량이 100Ah인 배터리의 남 은 용량이 80Ah인 경우 DoD =[(100−80)/100]×100=20%
예) 총 용량이 50Ah인 배터리의 현재 남은 용량이 30Ah인 경우 SoC = (30 /50)×100=60%
C-rate
배터리가 충전 또는 방전되는 속도를 나타냅니다.
1C에서 배터리는 표시된 Ah 정격과 동일한 전류로 충전 및 방전됩니다.
0.5C에서는 전류는 절반, 시간은 두 배,
0.1C에서는 전류는 1/10, 시간은 10배가 됩니다
그림 2와 그림 3은 일반적인 SoC 및 배터리 전류 프로파일에 대한 블록 E1 출력(DoD 및 C-rate)을 보여줍니다
Figure 2 DoD estimation during each cycle.
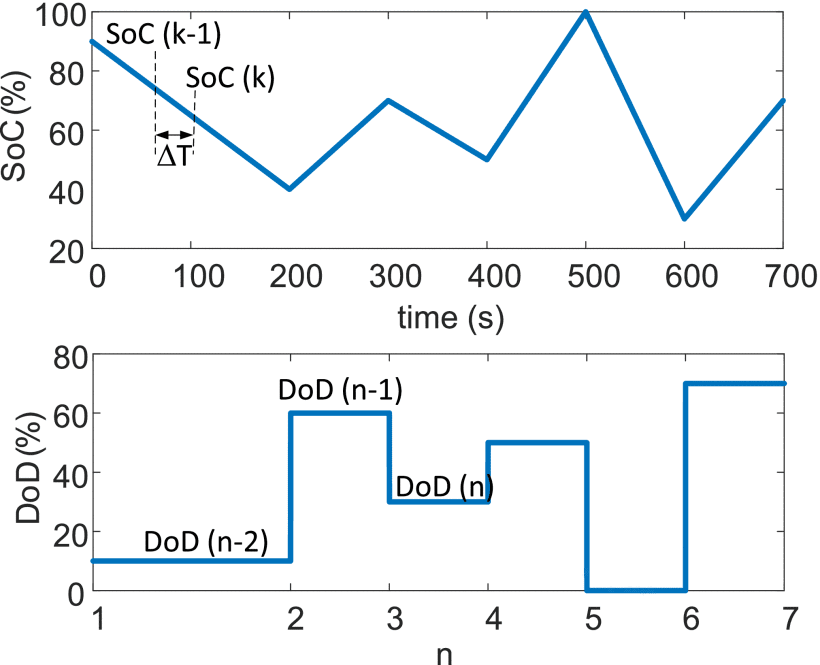
Figure 3. C-rate estimation during each cycle.
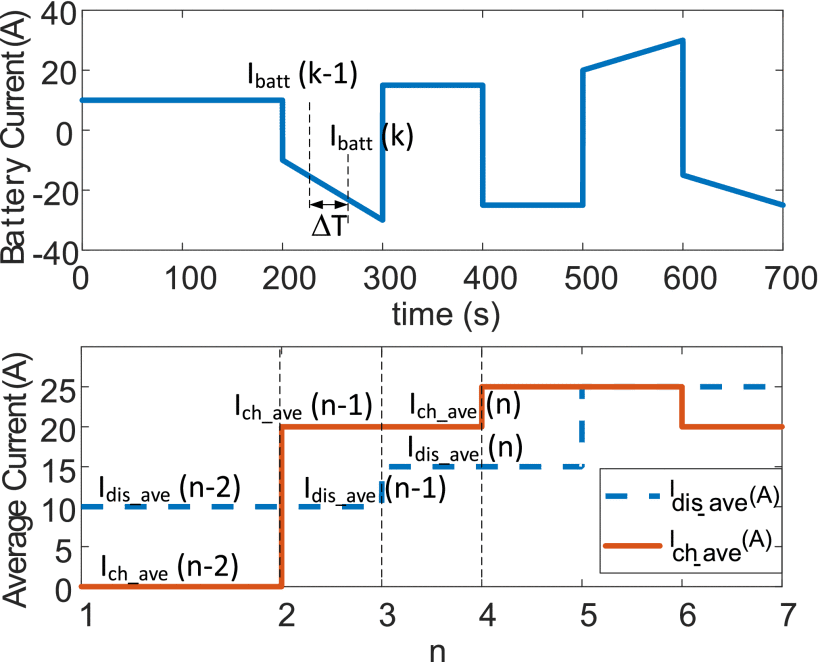
각 사이클 동안의 DoD는 배터리가 충전에서 방전으로 또는 방전에서 충전으로 전환될 때 계산됩니다.
이는 작은 시간 단계 ΔT에 대한 SoC(ΔSoC)의 변화를 살펴봄으로써 수행됩니다.
ΔSoC의 부호가 이전 시간 단계에서 계산된 것과 다를 때 전환이 감지됩니다.
방정식(1)은 모든 시간 단계 ΔT에서 SoC의 변화를 계산하는 데 사용됩니다. : (1) : K시점에 SoC 변화량
ΔSoC(k) = SoC(k) − SoC(k−1)
여기서, SoC (k)는 시간 k⋅ΔT (k = 1,2,3,.., ∞)에 샘플링된 SoC
n : transition
a : sample
k : time
DoD는 아래 알고리즘을 사용하여 계산
Step1: transitions의 갯수를 초기화, nprev = 1 과
DoD, DoD(1) = 1 – SoCinit, 여기서, SoCinit 은 배터리 초기 SoC.
Step 2: 모든 time step ΔT에서 ΔSoC(k)를 계산하다. 만약 ΔSoC(k) 부호≠ ΔSoC(k−1)부호 다르다면,
- Increment number of transitions, n = nprev + 1.
- Calculate DoD as follows, DoD(n)=1−SoC(k) (2)
- Store number of transitions, nprev=n.
각각 충/방전동안 [평균C-rates, Idis_ave , Ich_ave ]은 또한 아래 알고리즘에 따라 충방전, 방충전이 전환할때 계산된다.
Step 1: 초기화한다.
sample의 갯수 aprev = 0,
transitions 수, nprev = 1,
C-rates,
Idis_ave(1) = IBatt_init,
Ich_ave(1) = IBatt_init,
여기서 IBatt_init 은 배터리의 초기 current.
Step 2: 모든 시간 step ΔT, ΔSoC(k) 계산. 만약 ΔSoC(k) 부호≠ ΔSoC(k−1) 부호가 다르다면,
- Increment number of transitions, n = nprev + 1.
- Calculate number of samples, a = k.
- Calculate Idis_ave and Ich_ave as follows,
if ΔSoC(k) > 0
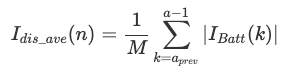
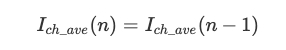
if ΔSoC(k) ≤ 0
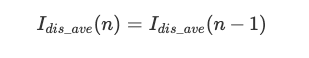
여기서 M= =a−aprev 은 두가지 전환간에 sample의 갯수
- Store the number of samples, aprev=a, and the number of transitions, nprev=n.
B. (블록 E2) 최대 사이클 수 추정
최대 사이클 수는 주어진 DoD, C-rate 및 온도에서 반복적인 방전 및 충전 사이클을 거쳤을 때,
배터리 수명이 다할 때까지(EoL: end-of-life)의 사이클 수로 정의됩니다.
배터리는 초기 용량의 20%가 손실되면 EoL에 도달한 것으로 간주됩니다.
7최대 사이클 수는 DoD, C-rate 및 온도에 의해 발생하는 스트레스 계수(또는 사이클당 스트레스)로부터 평가됩니다.
사이클링으로 인한 배터리 노화는 누적된 주기적 Stress으로 인한 재료 열화와 유사하며,
피로 분석의 방정식은 배터리 사이클 수명 연구에 적용할 수 있습니다. [33]에서 사이클당 성능 저하(D, Degradation per cycle)는
뵐러 근사법과 마이너의 법칙을 사용하여 다음과 같이 계산됩니다: (7)
여기서 σampl은 재료가 받는 Stress 진폭(stress amplitude)
σYield는 재료가 견딜 수 있는 최대 Stress(peak stress , 또는 항복 강도),
m은 피로 강도 지수(fatigue strength exponent)
비유하자면,
DoD로 인한 사이클당 stress의 진폭이 DoD(n)이고
피크 Stress 진폭이 즉 DoDref=100%인 경우,
DoD와 관련된 Stress 계수(θDoD)는 다음과 같이 계산할 수 있습니다: (8)
여기서, ξ DoD에 대한 Stress exponent (Stress 멱지수)
마찬가지로, C-rates으로 인한 Stress factor(스트레스 계수)를 계산해보면, (9)
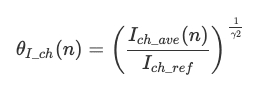
여기서 θI_dis(n) 및 θI_ch(n)은 각각 방전 및 충전 전류와 관련된 Stress 계수 stress factors
Idis_ref 및 Ich_ref 는 각각 방전 및 충전 전류의 피크 스트레스 진폭 peak stress amplitudes
γ1 및 γ2 는 각각 방전 및 충전 전류에 대한 스트레스 지수 stress exponents
온도에 따른 응력 계수(θT)는 아르헤니우스 방정식을 사용하여 [32]와 같이 계산합니다:
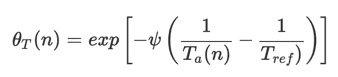
여기서
where Ta(n) and Tref are the ambient and reference temperatures, respectively, during each cycle. ψ is the Arrhenius rate constant.
The resulting or combined stress factor (θ) is computed as
여기서, Ta (n)및 Tref는 각각 사이클 동안의 주변온도및 기준온도
ψ 는 아레니우스비율상수 (Arrhenius rate constant )
결과로나온 또는 결합된 stress factor (θ) 는 다음과 같이 계산됩니다: [32]
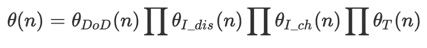
The maximum number of cycles (Nc) to EoL is inversely proportional to the resulting stress factor and is computed as [33]:
EoL까지 사이클의 최대수 (Nc)는 결과스트레스 계수에 반비례하면, 다음과 같이 계산된다.[33]:
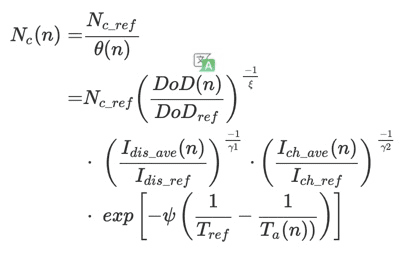
여기서 Nc_ref는 배터리에 방전 및 충전 사이클이 반복될 때의 최대 사이클 수
(DoD = DoDref, C-rates = (Idis_ref,Ich_ref), 온도 = Tref)인 조건으로
C. (블록 E3) 노화 지수 추정
aging index (노화 지수)는 배터리의 총 노화에 대한 “적용된 사이클의 기여도”를 나타냅니다.
배터리에 방전 및 충전 사이클이 반복되는 경우
(즉, 배터리가 100% SoC에서 0% SoC로 방전된 후 100% SoC로 재충전되는 경우),
한 사이클 후의 노화 지수는 다음과 같이 주어집니다: (14)
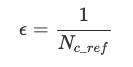
현실적인 부하 프로파일의 경우, 방전(또는 충전) 사이클이 항상 배터리 SoC 100%로 시작(또는 종료)되는 것은 아니라는 점을 고려하여 등가 사이클 수라는 개념을 도입했습니다.
주어진 DoD에 대한 등가 사이클 수는 사이클의 시작과 끝의 SoC가 100%인 시나리오에 해당하는 사이클 수로 정의됩니다.
예를 들어, 배터리가 80% SoC( 20% DoD)에서 40% SoC(60% DoD)로 방전되었다가 60% SoC(40% DoD)로 재충전된 경우입니다. 이 사이클의 DoD는 60%이며 이에 상응하는 사이클 수는 (그림 4 참조)로 표시됩니다: (15)
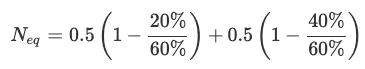
Figure 4. Equivalent number of cycle concept.
(13)은 100% SoC로 시작하고 끝나는 사이클에만 적용되므로,
동등한 사이클 수라는 개념을 통해 배터리가 특정 DoD 스윙을 받을 때 노화 지수를 계산할 수 있습니다.
그림 2에 (15)를 적용하면 각 사이클 이후의 등가 사이클 수는 다음과 같이 계산됩니다: (16)
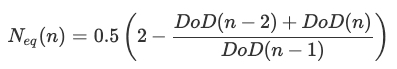
각 사이클후에 aging index 는 아래와 같다: (17)
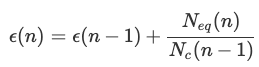
D. (블록 E4) 배터리 용량 및 저항 추정
배터리 용량과 저항은 노화 지수를 기반으로 결정됩니다.
[34]에서 설명한 바와 같이, 배터리 용량과 저항은 노화에 따라 비선형적인 특성을 보입니다.
이는 주로 배터리가 노화됨에 따라 고체 전해질 간상(SEI) 층의 비선형 성장과 리튬 이온, 활물질 및 전해질의 비선형 손실로 인해 발생합니다.
배터리 용량(Q)과 저항(R)은 (노화의 비선형 효과를 고려하여) 다음과 같이 표현할 수 있습니다
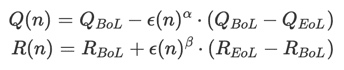
여기서, QBoL 및 QEoL은 각각 BoL(수명 시작 시점) 및 EoL에서의 배터리 용량(Ah)입니다.
RBoL 및 REoL은 각각 BoL 및 EoL에서의 배터리 저항(Ω)입니다.
α와 β는 각각 배터리 용량과 저항에 대한 노화 지수입니다.
QEoL은 QBoL의 80%로 가정합니다.
QBoL 및 RBoL은 각각 블록 D의 Q(T) 및 R(T)에 해당합니다(그림 1 참조).
섹션 III: 모델 파라미터의 식별
방정식 (13)은 5개의 매개변수(Nc_ref, ξ, γ1, γ2, ψ)를 식별해야 합니다.
이러한 파라미터는 다양한 사이클링 조건에서 수명 주기 곡선(용량 손실 대 사이클)을 사용하여 결정됩니다.
배터리 데이터시트와 제한된(또는 짧은 기간의) 사이클링 실험을 통해 모델 파라미터를 파악합니다.
- Battery datasheet
- (limited (or short duration) cycling) Experiments
용량이 5% 감소할 때까지 4개의 배터리를 동시에 다른 조건에서 순환시키는 것으로 구성됩니다.
각 사이클링 조건마다 개별 효과를 감지하기 위해 하나의 사이클 수명 인자(DoD, C-rate 또는 온도)만 변경됩니다.
5%라는 숫자는 각 사이클 수명 인자가 배터리 노화 과정에 미치는 영향을 파악하기 위해 선택되었습니다.
노화 지수(α 및 β)는 공칭 사이클링 조건에서의 용량 손실 및 저항 증가 곡선으로부터도 결정됩니다. 저항 증가 곡선(저항 대 사이클)은 데이터시트에 거의 제공되지 않기 때문에 배터리 저항은 몇 번의 사이클마다 실험적으로 측정됩니다.
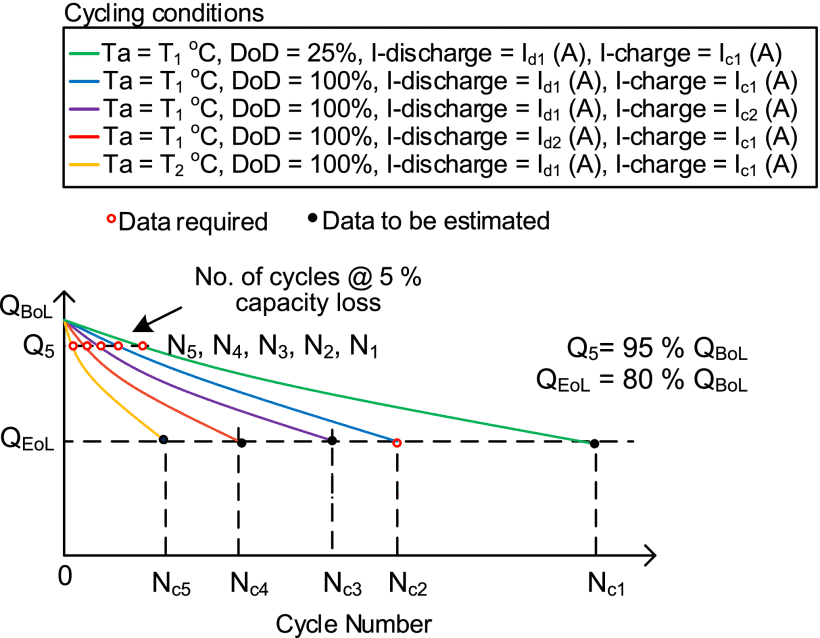
그림 5는 데이터시트 또는 실험에서 필요한 일반적인 데이터 포인트를 보여줍니다. 그림에서 볼 수 있듯이(파란색 곡선 참조), 적어도 하나의 전체 수명 주기 곡선(즉, EoL까지 배터리 사이클링)이 필요합니다. 이 데이터는 대부분의 데이터시트에서 검색할 수 있으므로 전체 수명 주기 테스트가 필요하지 않습니다. 따라서 사이클 실험에 소요되는 시간을 줄일 수 있습니다.
Figure 5. Typical data points required for model parameters identification. Red dots indicates extracted data points and black dots are estimated data.
The aging exponent, α, is estimated using (18), at nominal cycling condition (Ta = T1 oC, DoD = 100%, I-discharge = Id1, I-charge = Ic1), as follows:
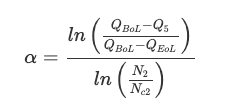
Similarly, β is given (using (19)) as:
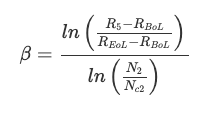
여기서 Q5는 QBoL의 95%입니다. N2 및 Nc2는 각각 용량이 Q5 및 QEoL일 때의 사이클 수입니다.
R5는 용량이 Q5일 때의 배터리 저항입니다.
다른 사이클링 조건에 대한 EoL(Nc1, Nc3, Nc4, Nc5)까지의 사이클 수는 (18)을 사용하여 추정합니다: (22)
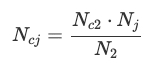
여기서 j∈(1,3,4,5). Nj는 그림 5와 같이 각 사이클링 조건에 대해 용량이 Q5일 때의 사이클 수입니다.
모델 매개변수(Nc_ref, ξ, γ1, γ2, ψ)는 식 (13)을 사용하여 다음과 같이 추정합니다:
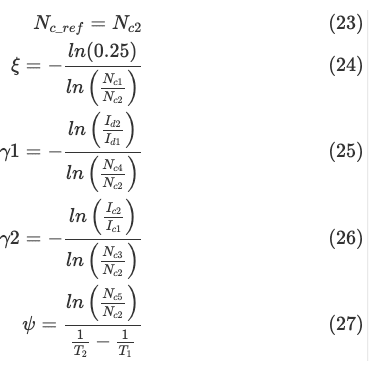
섹션 4: 실험적 검증
제안된 사이클 수명 모델은 두 가지 리튬 이온 배터리 화학 물질(LFP-LiFePO4 및 NMC-LiNiMnCoO2)을 사용하여 검증됩니다. 검증을 위해 열 테스트 챔버가 포함된 테스트 벤치를 사용하여 다양한 사이클링 조건에서 가속 사이클링 테스트를 수행합니다.
그림 5에서 볼 수 있듯이 모델 파라미터 식별을 위해서는 최소 4개의 수명 주기 곡선이 필요합니다
(배터리 데이터시트에서 사용 가능한 데이터에 따라 테스트 횟수를 줄일 수 있음).
다음 섹션에서는 테스트 벤치 설정에 대해 간략하게 설명합니다(그림 6 참조).
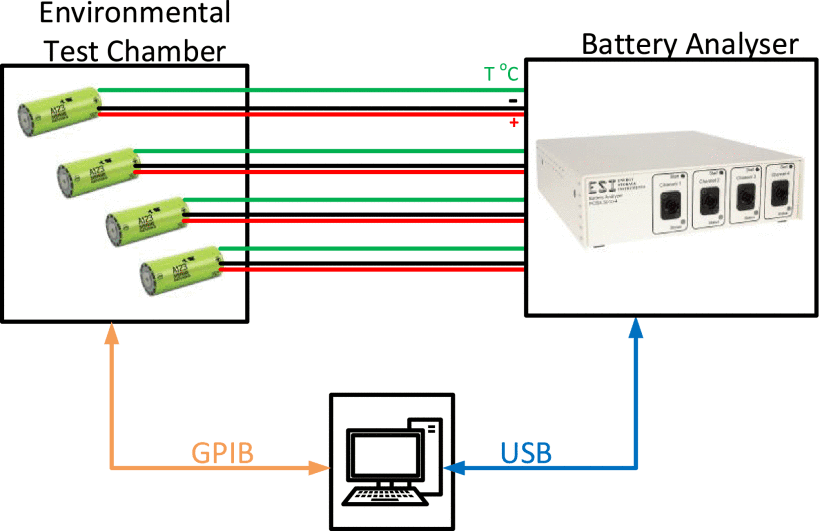
A. 테스트 벤치 설정
테스트 벤치 설정은 다음과 같이 구성됩니다:
- 환경 테스트 챔버(써모트론 XSE-600).
- 최대 4개의 배터리 셀을 동시에 순환시킬 수 있는 4채널 배터리 분석기/사이클러(PCBA 5010-4).
- A123 시스템의 5개의 LiFePO4 배터리 셀, 3.3V, 2.5Ah, 26650 원통형.
- 리튬이온코발트수소 배터리 셀 5개, 3.7V, 2000mAh, 18650 원통형 일반 배터리.
LiFePO4 배터리의 경우, 데이터시트 및 실험 테스트의 수명 주기 곡선을 사용하여 모델 파라미터를 식별합니다.
사이클 조건은 표 I에 요약되어 있습니다.
표 1. 파라미터 식별을 위한 사이클링 조건, LiFePO4 배터리
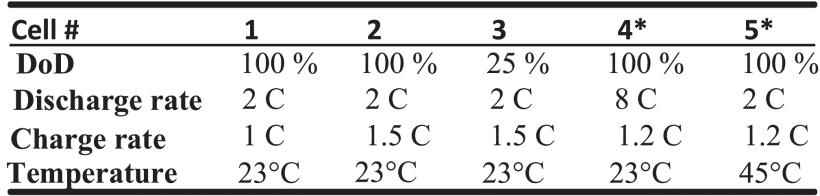
표 I에서 볼 수 있듯이, LiFePO4 배터리는 상온에서 세 가지 실험 테스트가 필요합니다.
각 사이클링 테스트는 용량 및 저항 테스트로 시작하여 BoL 용량과 저항을 결정합니다.
매 Δn 사이클 수(Δn은 BoL 및 EoL 근처에서 5 사이클, 그 사이에서 50 사이클)마다 사이클이 중단되고 용량 및 저항 테스트가 시작되어 현재 용량 및 저항을 결정합니다.
용량이 초기 값의 95%에 도달할 때까지 테스트 순서가 계속됩니다.
새 LFP 배터리 셀을 순환하는 동안 용량이 증가하다가 처음 몇 사이클(50~100사이클) 동안 공칭 값으로 떨어집니다.
NMC의 경우 이 현상은 눈에 띄지 않았습니다. 이 현상이 완료되는 즉시, 즉 배터리가 노화되기 시작하면 데이터 기록이 시작되었습니다.
그림 7-10은 표 I의 사이클링 조건에서 시뮬레이션 및 실험 결과를 보여줍니다.
그림에서 볼 수 있듯이, 각 수명 주기 요인이 리튬이온 배터리에 미치는 영향은 제안된 모델에 의해 1% 미만의 절대 오차로 잘 표현됩니다.
Figure 7. Impact of discharge C-rate on the LFP battery life cycle
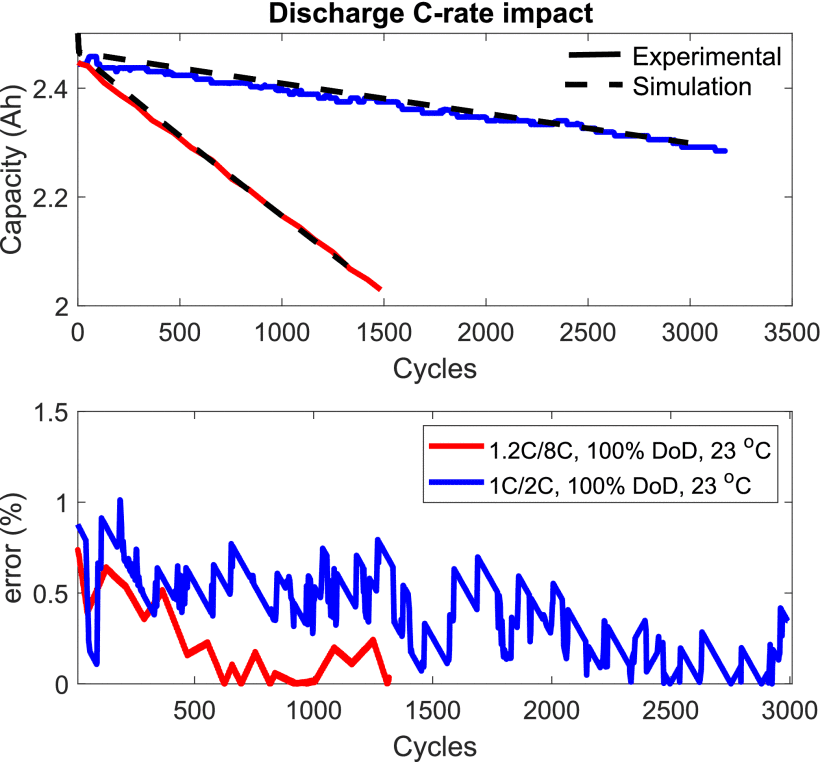
Figure 8.Impact of charge C-rate on the LFP battery life cycle.
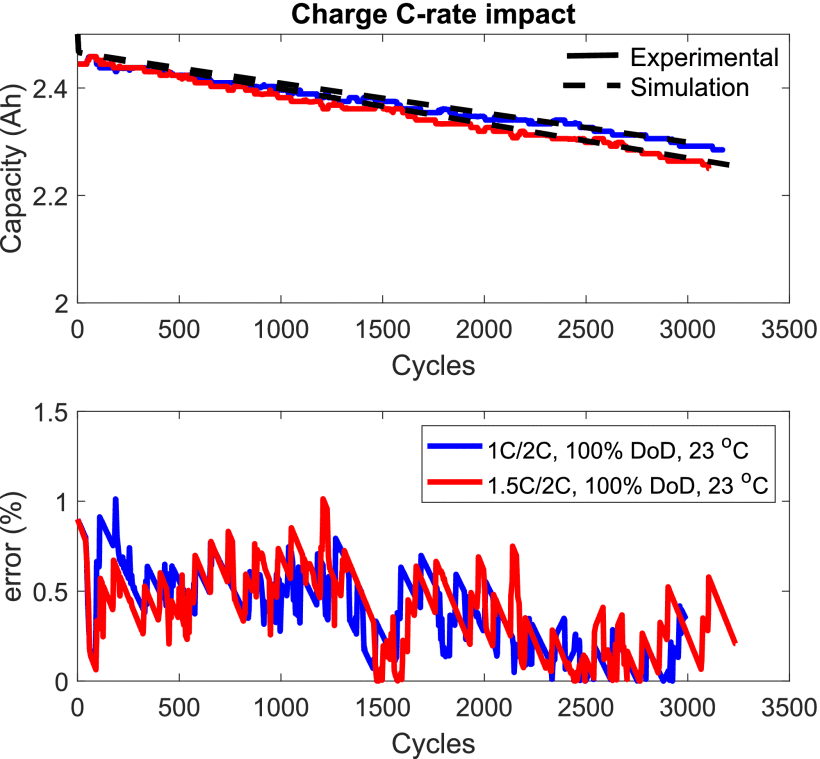
Figure 9.Impact of DoD on the LFP battery life cycle.
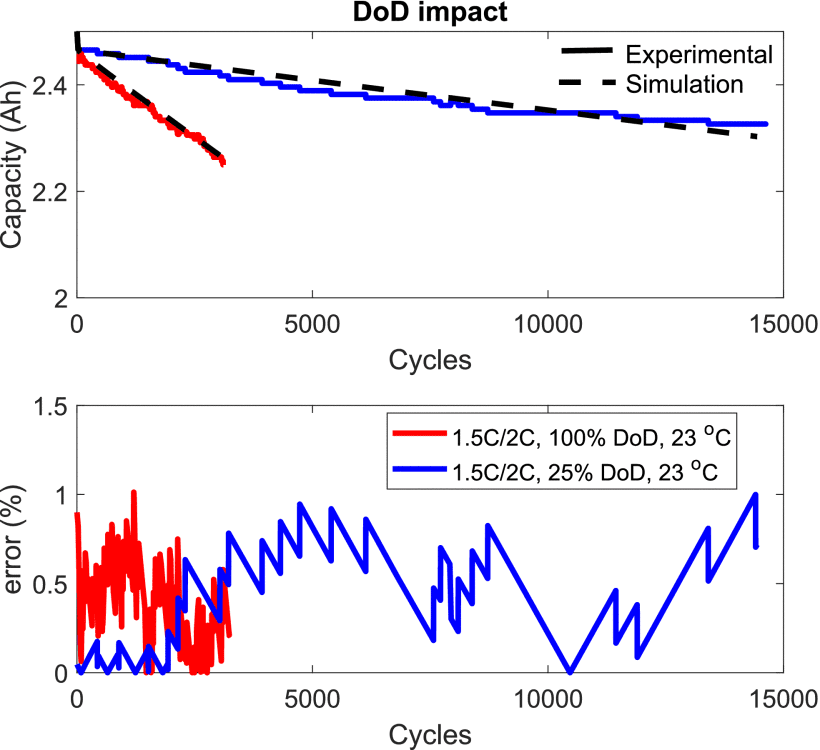
Figure 10.Impact of ambient temperature on the LFP battery life cycle.
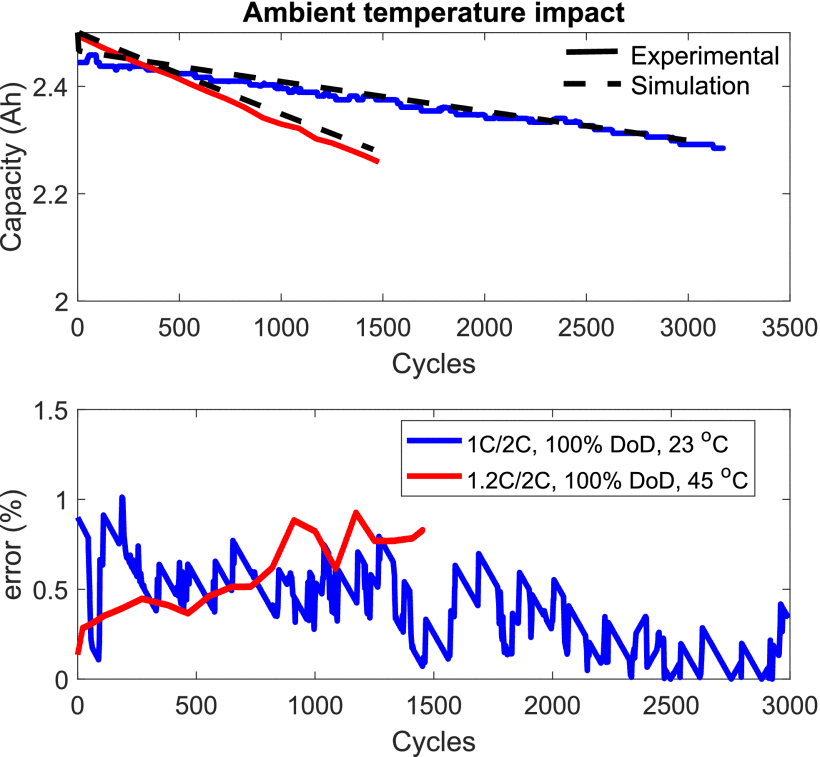
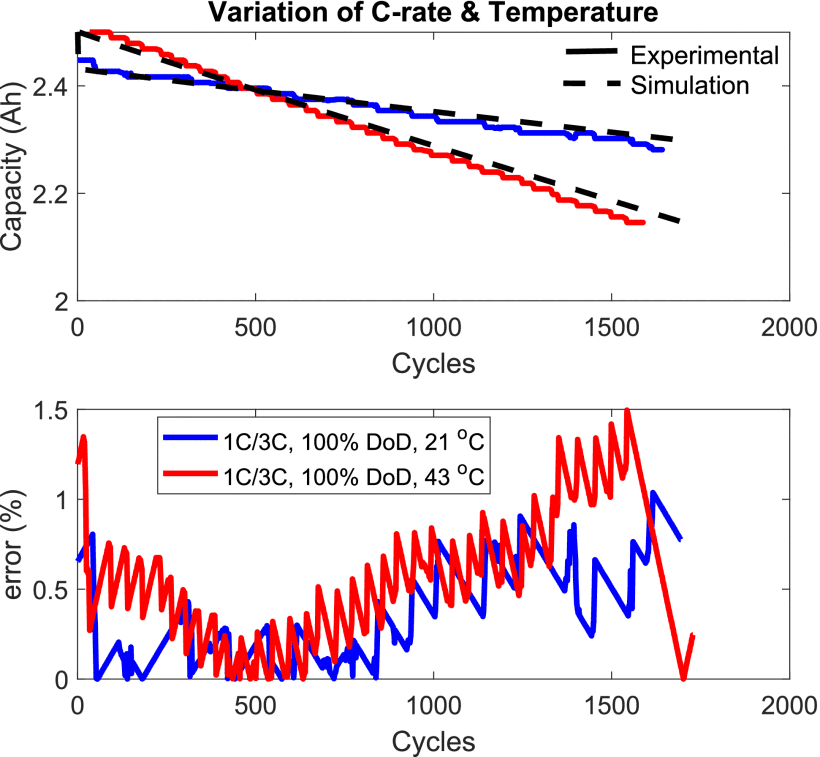
표 II는 데이터시트 및 실험에서 추출한 데이터와 모델 파라미터를 LFP 배터리 유형에 대해 보여줍니다. 그림 11은 국방부, C-rate 및 주변 온도에 따른 사이클당 예상 스트레스 요인을 보여줍니다.
Table 2. Model Parameters for the LFP Battery
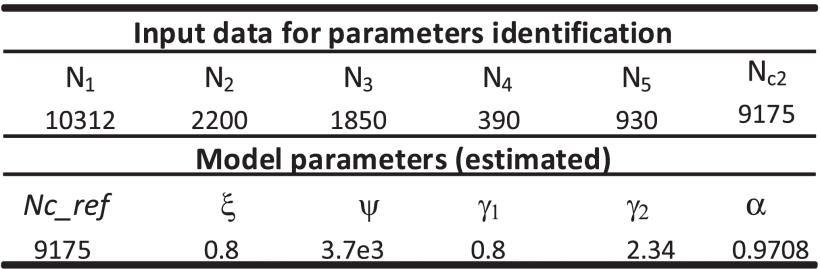
검증을 위해 파라미터 식별에 사용된 조건과 다른 작동 조건에서 두 가지 추가 사이클링 테스트를 수행했습니다.
그림 12는 21°C 및 43°C 주변 온도에서 1C(충전)/3C(방전)의 C-rate로 LFP 배터리를 100% DoD로 사이클링했을 때의 시뮬레이션 및 실험 결과를 보여줍니다. 그림에서 보는 바와 같이 21°C와 43°C에서 각각 최대 절대 오차가 1%와 1.5%로 현실에 가까운 결과를 확인할 수 있습니다.
Figure 12. Model performance at different cycling conditions.
NMC 배터리의 경우, 표 III에 표시된 대로 5번의 사이클링 테스트에서 모델 파라미터를 추출했습니다.
테스트는 LFP 배터리와 동일한 방식으로 진행되었습니다.
Table 3. Cycling Conditions for Parameters Identification, LiNiMnCoO2 Battery

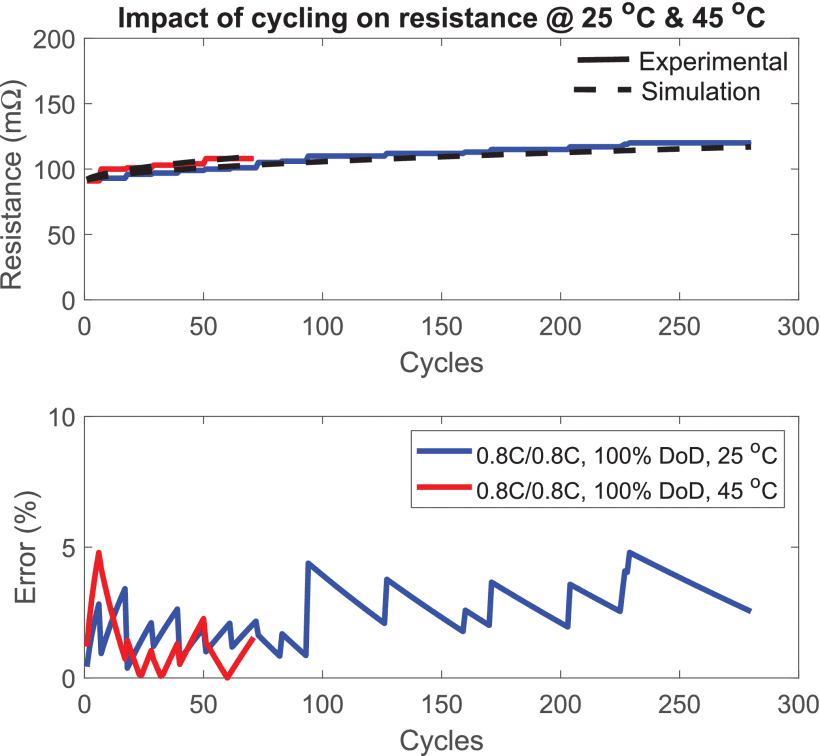
실험 결과, LFP 배터리의 경우 배터리 저항이 크게 변하지 않은 반면, NMC의 경우 EoL에서 39% 증가한 것으로 나타났습니다. NMC 배터리의 저항 증가 결과는 그림 17-18에 나와 있습니다.
노화 지수 β = 0.5262(R5 = 108mΩ, RBoL = 90mΩ 및 REoL = 125mΩ으로 (21)을 사용하여 계산).
그림 17-18에서 볼 수 있듯이, 제안된 모델은 배터리 저항에 대한 사이클링의 영향을 5% 미만의 절대 오차로 나타낼 수 있습니다.
FIGURE 17. Impact of cycling at 0.8 C and 1.5 C discharge C-rates on battery resistance.
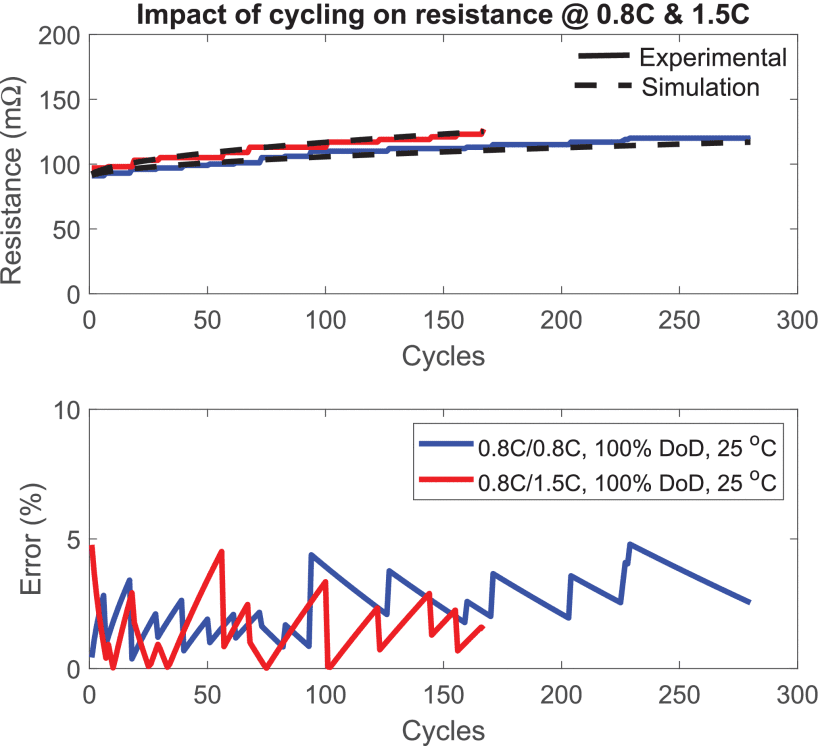
FIGURE 18. Impact of cycling at 25 ◦C and 45 ◦C ambient temperatures on battery resistance.
섹션 V. 결론
본 논문에서는 리튬 이온 배터리의 사이클 수명 모델을 제시했습니다.
이 모델은 피로 분석에 일반적으로 사용되는 물리 방정식과 등가 사이클 카운팅을 기반으로 하므로 모든 리튬 이온 배터리 유형에 적용할 수 있습니다.
배터리 데이터시트와 제한된 (짧은 기간의) 사이클 테스트를 사용하여 매개변수 식별 프로세스를 간소화하는 것이 주요 특징입니다.
대부분의 리튬 이온 배터리 데이터시트에는 수명 주기 곡선이 포함되어 있기 때문에, 파라미터 식별 프로세스에 소요되는 시간과 비용이 줄어듭니다. 이 모델은 방전 깊이(DoD), 온도, C-rate과 같은 일반적인 사이클 수명 요소의 영향을 나타낼 수 있습니다.
두 가지 리튬 이온 배터리 유형(LFP-LiFePO4 및 NMC-LiNiMnCoO2)에 대한 시뮬레이션 결과는 배터리 용량에 대한 절대 오차가 1.5% 미만으로 현실에 가깝습니다. 이 모델은 배터리 저항에 대해서도 5% 미만의 절대 오차를 제공했습니다.
따라서 제안된 모델은 리튬 이온 배터리 사이클링 효과의 전기적 시뮬레이션을 위한 좋은 후보가 될 수 있습니다.