PCA eigen 관계
# Data from https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
# n1 n2 n3 n4 n5
# p1 0.2 ,0.45,0.33,0.54,0.77
# p2 5.6 ,5.89,6.37,7.9 ,7.87
# p3 3.56,2.4 ,1.95,1.32,0.98
Xorigin <- data.frame(p1=c(0.2 ,0.45,0.33,0.54,0.77), p2=c(5.6 ,5.89,6.37,7.9 ,7.87), p3=c(3.56,2.4 ,1.95,1.32,0.98))
Xmatrix0 <- data.matrix(Xorigin)
# centering ----------------------------------------------------------------
Xorigin_centering <- data.frame(lapply(Xorigin, function(x){((x-mean(x)))}))
Xmatrix1 <- data.matrix(Xorigin_centering)
sigma1 <- cov(Xmatrix1)
# normalizing ------------------------------------------------------------------------
Xorigin_centering_scale <- data.frame(lapply(Xorigin,function(x){((x-mean(x))/sd(x))}))
Xmatrix2 <- data.matrix(Xorigin_centering_scale)
sigma2 <- cov(Xmatrix2)
# Prcomp in r ------------------------------------------------------------------------
pr_c <- prcomp(Xmatrix0, center=T) # Xmatrix1
pr_c$sdev^2 # eigen(sigma1)$values # 분산 설명력
pr_c$rotation # eigen(sigma1)$vectors*-1 # New 축
pr_c$x # Xmatrix1 %*% eigen(sigma1)$vectors*-1 # New 좌표 predict(pr_c) identical(A,B)
pr_cs <- prcomp(Xmatrix0, center=T, scale=T) # Xmatrix2
pr_cs$sdev^2 # eigen(sigma2)$values
pr_cs$rotation # eigen(sigma2)$vectors*-1
pr_cs$x # Xmatrix2 %*% eigen(sigma2)$vectors
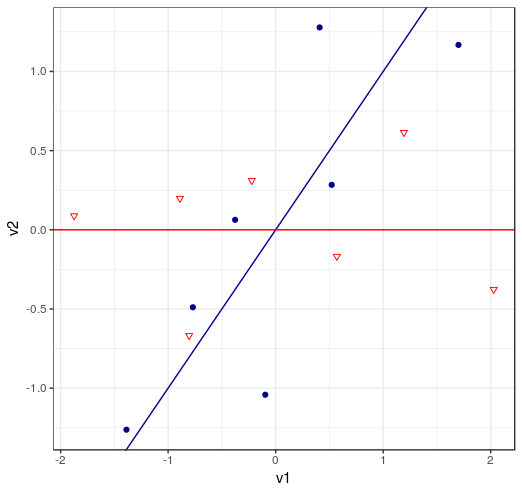
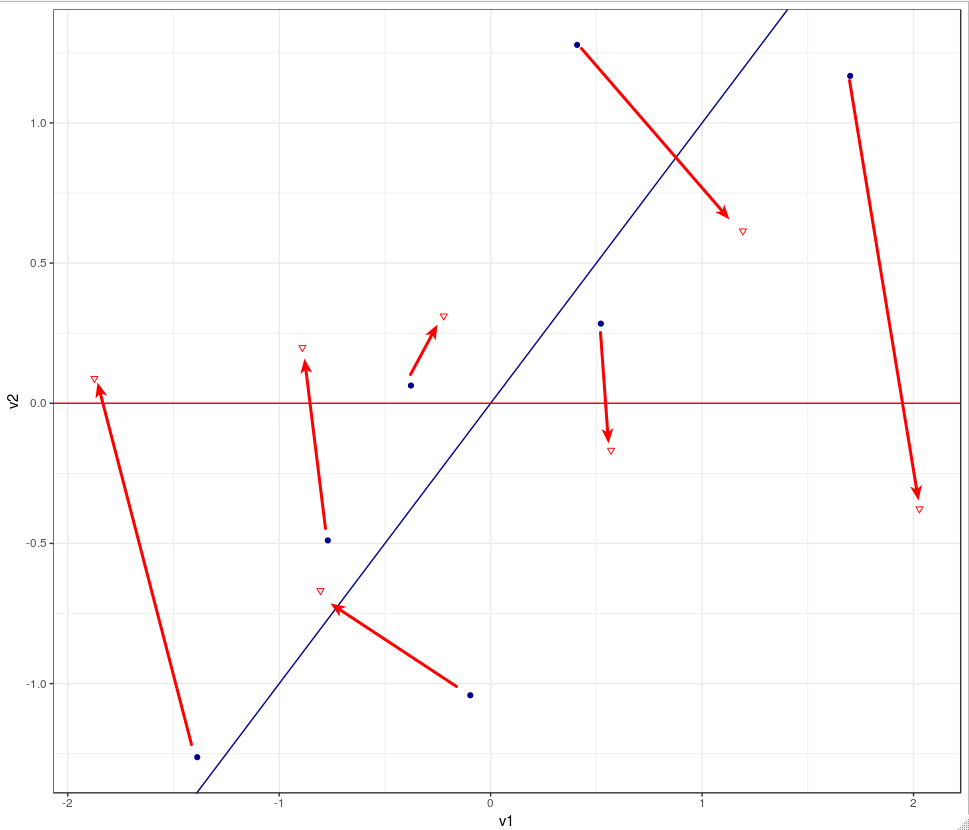
선형변환을 통해, 분산을 최대이고 직교하는 새로운 축을 기준으로 Projection한다.
이를통해 고차원(2차)–> 저차원, 기존 V1,V2에서 PC1,PC2의 새로운 변수추출이 가능하다.
Xorigin <- data.frame(v1=c(22,45,33,54,77,56,40), v2=c(56,58,63,79,78,70,68))
(p <- ggplot(Xorigin) + geom_point(aes(x=v1, y=v2, color="skyblue")) +theme_bw())
Xorigin_centering_scale <- data.frame(lapply(Xorigin,function(x){((x-mean(x))/sd(x))}))
Xmatrix2 <- data.matrix(Xorigin_centering_scale)
(p_n <- ggplot(Xorigin_centering_scale, aes(x=v1, y=v2)) + geom_point(color='darkblue')+ geom_abline(color='darkblue'))
pr_cs <- prcomp(Xorigin, center=T, scale=T) #Xmatrix2
pr_cs$sdev^2 # eigen(sigma2)$values
pr_cs$rotation # eigen(sigma2)$vectors*-1
pr_cs$x # Xmatrix2 %*% eigen(sigma2)$vectors
(p_pc <- p_n + geom_point(data.frame(pr_cs$x), aes(x=PC1, y=PC2), color='red', shape=6) +
geom_hline(yintercept = 0, color= 'red') + theme_bw())